1.
a)
x² + 4x + 10 ≥ 0
Рассмотрим функцию у = x² + 4x + 10.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² + 4x + 10 = 0
D = 16 - 40 = - 24 < 0
нулей нет, значит график не пересекает ось Ох.
Схематически график изображен на рис. 1.
у > 0 при x ∈ (- ∞; + ∞)
ответ: 2) Решением неравенства является вся числовая прямая.
b)
- x² + 10x - 25 > 0 | · (- 1)
x² - 10x + 25 < 0
Рассмотрим функцию у = x² - 10x + 25.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² - 10x + 25 = 0
(x - 5)² = 0
x = 5
Схематически график изображен на рис. 2.
у < 0 при x ∈ {∅}
ответ: 1) Неравенство не имеет решений.
c)
x² + 3x + 2 ≤ 0
Рассмотрим функцию у = x² + 3x + 2.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² + 3x + 2 = 0
D = 9 - 8 = 1
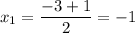
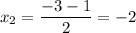
Схематически график изображен на рис. 3.
у ≤ 0 при x ∈ [- 2; - 1]
ответ: 4) Решением неравенства является закрытый промежуток.
d)
- x² + 4 < 0 | · (- 1)
x² - 4 > 0
Рассмотрим функцию у = x² - 4.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² - 4 = 0
x² = 4
x = ± 2
Схематически график изображен на рис. 4.
у > 0 при x ∈ (- ∞; - 2) ∪ (2; + ∞)
ответ: 6) Решением неравенства является объединение двух промежутков.
___________________________
2.
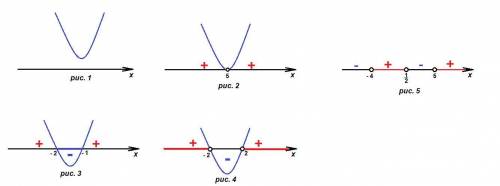
(x - a)(2x - 1)(x + b) > 0
x ∈(- 4; 1/2) ∪ (5; + ∞)
Решение неравенства показано на рис. 5.
Найдем нули функции у = (x - a)(2x - 1)(x + b).
(x - a)(2x - 1)(x + b) = 0
(x - a) = 0 или (2x - 1) = 0 или (x + b) = 0
x = a x = 1/2 x = - b
Из решения неравенства следует, что нулями являются числа - 4, 1/2 и 5. Значит
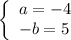 или
или 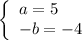
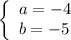 или
или 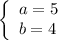
ответ: a = - 4, b = - 5 или a = 5, b = 4.
Примем длину дороги ( кольца) за S метров
Пусть скорость одного автомобиля V₁, другого V₂
Тогда при движении в одном направлении скорость отдаления
=V₁-V₂,
а
S=1 ч(V₁-V₂)
Cкорость сближения при движении в противоположных направлениях
V₁+V₁, и
S=0,5(V₁+V₂)
Cоставим систему
|1 ч(V₁-V₂)=S
|0,5(V₁+V₂) =S умножим это уравнение на 2
|V₁-V₂=S
|V₁+V₂=2S сложим уравнения
получим
2V₁=3S
v₁=1,5 S
Подставим это значение в
V₁-V₂=S
1,5 S - V₂=S
V₂=2,5 S
Найдем время, за которое проедет всю кольцевую трассу каждый автомобиль
t=S:v
t₁=S:v₁=S:1,5 S=1:1,5=10/15=2/3 часа или 40 мин
t₂=S:v₂=S:2,5=1:2,5=10/25=2/5 часа или 24 мин
2x²+5x-3-2x²-2x-8=0
3x-11=0
3x=11