ОДЗ:
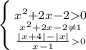
Решаем каждое неравенство:
⇒ 
⇒
⇒ 
⇒ 
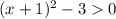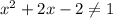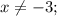
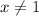
Подмодульные выражения обращаются в 0 в точках
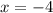и 
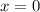
Это точки делят числовую прямую на три промежутка.
Раскрываем знак модуля на промежутках:
(-∞;-4]
|x+4|=-x-4
|x|=-x
⇒ 
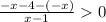⇒ x < 1
решение неравенства (-∞;-4]
(-4;0]
|x+4|=x+4
|x|=-x
⇒ 
⇒ x < -2 или x > 1
решение неравенства (-4;-2)
(0;+∞)
|x+4|=x+4
|x|=x
⇒ 
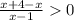⇒ x > 1
решение неравенства (1;+∞]
Объединяем ответы трех случаев:
при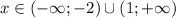 
ОДЗ:
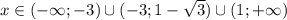
Решаем неравенство: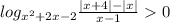 
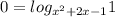
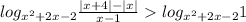
Два случая:
если основание логарифмической функции >1, то она возрастает и большему значению функции соответствует большее значение аргумента
⇒ 
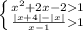⇒ ![\left \{ {{x\in (-\infty;-3) \cup(1;+\infty)} \atop {x\in(-\infty;-4]\cup(1;5)}} \right.](/tpl/images/1360/8793/82812.png)
второе неравенство решаем на промежутках так:
(-∞;-4]
⇒ 
⇒ 
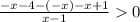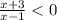⇒ (-3;-1)
не принадлежат (-∞;-4]
на (-4;0]
⇒ 
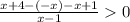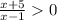⇒ x < -5 или x > 1
не принадлежат (-4;0]
(0;+∞)
⇒ 
⇒ 
⇒
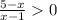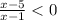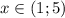
о т в е т этого случая 
если основание логарифмической функции 0 < a < 1, то она убывает и большему значению функции соответствует меньшее значение аргумента
⇒ 
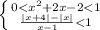⇒ ![\left \{ {{x\in (-3;-1-\sqrt{3}) \cup(-1+\sqrt{3};1)} \atop {x\in(-\infty;-4]\cup(-4;0]\cup(5;+\infty)}} \right.](/tpl/images/1360/8793/ac205.png)
второе неравенство решаем на промежутках так:
(-∞;-4]
⇒ 
⇒ 
⇒
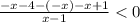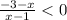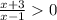(-∞;-3)U(1;+∞)
о т в е т. (-∞;-4]
на (-4;0]
⇒ 
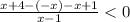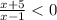⇒ -5 < x < 1
о т в е т. (-4;0]
(0;+∞)
⇒ 
⇒ 
⇒
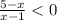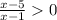о т в е т этого случая 
С учетом ОДЗ получаем окончательный ответ: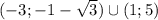
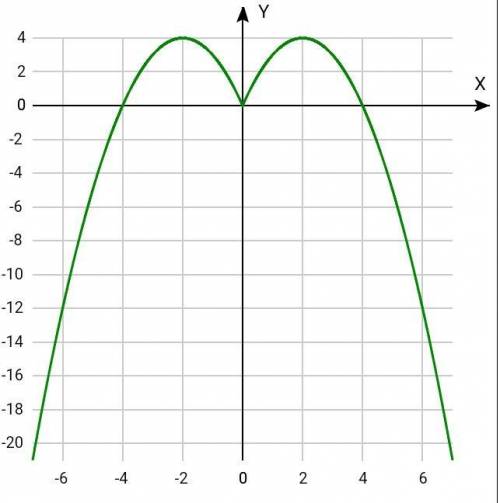
f(x) = 4|x| - x²
1. D(f) = R - симметрична относительно 0.
2. f(-x) = 4|-x| - (-x)² = 4|x| - x² = = f(x),
по определению f(x) - чётнвя.
График чётной функции симметричен относительно оси Оу.
3. Построим часть графика для х ≥ 0, а затем отобразим построенную часть симметрично относительно оси Оу.
f(x) = 4x - x² - квадратичная, графиком является парабола, ветви направлены вниз, т.к. а = - 1, а<0.
х вершины = - b/(2a) = -4/(-2) = 2;
у вершины = 4•2 - 2² = 4;
(2;4) - вершина параболы.
Найдём нули функции:
4x - x² = 0
- х (х - 4) = 0
х = 0 или х = 4
(0;0) и (4;0) - точки пересечения с осью Ох.
Изображение графика смотрите в прикреплённом чертеже.
t6+q6+1>0, если t и q принадлежат [-1;+бесконечности]
Представляешь значения от -1 до бесконечности и убеждаешься. Например
Пусть t=-1,а q=5, то t6+q6+1=-1*6+5*6+1=25.
Можешь проверить с другими значениями, ответ будет положителен в любом случае. Я не знаю как это правильно оформить как могла.