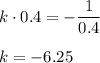
72км
Объяснение:
1-й мотоциклист, проехав расстояние от А до В, повернул и проехал от В 12км, пока не встретил 2-го мотоциклиста. Возьмем х за расстояние, которое проехал 2-й мотоциклист до встречи с 1-м. Следовательно расстояние от А до В, которое возьмем за у будет равным:
у=х+12.
Когда на обратном пути 1-й мотоциклист, проехав (1/6 у)км расстояния от А, встречает 2-го мотоциклиста (не обгоняет!). Значит расстояние между А и В будет равным:
у=х +1/6 у.
Составляем систему уравнений:
у=х+12
у=х +1/6 у
х+12-х -1/6 у=у-у
12 -1/6 у=0
1/6 у=12
у=12•6=72км - расстояние между пунктами А и В.
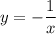и затем верхнюю часть графика отобразить в нижнюю(отрицательную часть)
(*)
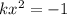и это уравнение решений не имеет при k>0(так как левая часть всегда положительно).
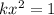и при k<0 это уравнение решений не имеет.
, имеем
