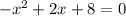
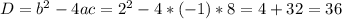
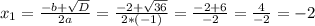
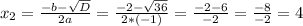
Область определения - это допустимые значения Х -обозначается D(y)/.
а) прямая - Х любое или D(y) - Х∈(-∞; +∞)
б) квадратичная функция - Х∈R или Х∈(-∞; +∞) - Х любое.
в) Если У= 2х/( 5 - х), то все кроме Х = 5 - деление на 0 не допускается - значение Х=5 исключается.
Записывается D(y)- Х∈(-∞;5)∪ (5;+∞)
Внимание: Х=5 не может быть - обозначаем круглой скобкой.
г) Произведение двух чисел. Х = любое.
д) У = 1/х² +1 - Все кроме Х=0 - деление на 0.
Х ∈ (-∞;0)∪(0;+∞)
е) Квадратный корень не может быть из отрицательного числа. Х ≥0.
D(y) - X∈[0;+∞).
Внимание: значение Х=0 может быть - в записи квадратная скобка.
Объяснение:
Координата точки записывается следующим образом: сначала записывается значение по оси Ox, потом значение по оси Oy.
Точка A с координатами (xₐ, yₐ) лежит на прямой, если при подстановке ее координат в уравнение прямой получается верное равенство.
В нашей задаче прямая задана уравнением 3x - 4y = 48
1) Проверим принадлежность точки A(20, 2) данной прямой
3 × 20 - 4 × 2 = 60 - 8 = 52
52 ≠ 48 ⇒ точка A(20, 2) не принадлежит прямой
2) Проверим принадлежность точки B(24, 6)
24 × 3 - 4 × 6 = 72 - 24 = 48
48 = 48 ⇒ Точка B(24, 6) принадлежит заданной прямой