Пусть х см - ширина прямоугольника. Тогда, (х+4) см - длина прямоугольника. Составим уравнение:
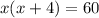
Раскроем скобки и перенесем все в левую часть:
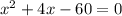
Решать уравнение будем по формуле корней для уравнения с четным вторым коэффициентом:
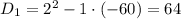
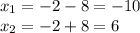
Поскольку сторона не может выражаться отрицательным числом, то первый корень не удовлетворяет условию задачи. Тогда:
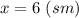 - ширина прямоугольника
- ширина прямоугольника
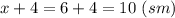 - длина прямоугольника
- длина прямоугольника
Составим выражения для периметра:
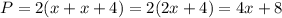
Находим периметр:
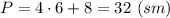
ответ: стороны прямоугольника 6 см и 10 см; периметр прямоугольника 32 см
решить уравнение (x²+x+1)*(x²+x+2) - 12=0
замена : t =x² + x + 1,5 * * * (1+2)/2 =1,5 * * *
(t - 0,5)*(t + 0,5)-12 =0 ⇔t² - 12,25 =0 ⇔(t +3,5)(t-3,5) =0 ⇒t₁= -3,5 ; t₂=3,5.
Обратная замена
a) x² + x + 1,5 = -3,5 ⇔ x² + x + 5 =0; D = (-1)² -4*1*5 = -19 < 0 не имеет
действительных корней * * * [ x =(-1 -i√19)/2 ; x =(-1 +i√19)/2 * * *
a) x² + x + 1,5 = 3,5 ⇔ x² + x - 2 = 0 ⇒x₁= -2 ; x₂=1.
ответ: { - 2 ; 1}
* * * можно и t = x² + x + 1 или t = x² + x + 1 * * *