Система уравнений имеет два решения:
1)[(1-2√3/2 (≈ -1,5); 7-4√3/2 (≈2,1)];
2)[1+2√3/2 (≈3,5); 7+4√3/2 (≈11,9)].
Объяснение:
Определите графически количество решение системы уравнений:
y=x²
y-2x-5=0
Преобразуем второе уравнение в уравнение функции:
y-2x-5=0
у=2х+5
Построим графики функций. Первый - парабола с вершиной в начале координат, ветви направлены вверх; второй - прямая линия.
Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу.
y=x² у=2х+5
Таблицы:
х -3 -2 -1 0 1 2 3 х -1 0 1
у 9 4 1 0 1 4 9 у 3 5 7
На графике прямая у=2х+5 пересекает параболу в двух точках, но значения очень приблизительные.
Определим координаты этих точек расчётами.
Приравняем правые части уравнений (левые равны) и вычислим х:
x²=2х+5
x²-2х-5=0, квадратное уравнение, ищем корни:
х₁,₂=(2±√4+20)/2
х₁,₂=(2±√24)/2
х₁,₂=(2±√16*3/2)/2
х₁,₂=(2±4√3/2)/2
х₁=1-2√3/2 (≈ -1,5)
х₂=1+2√3/2 (≈3,5)
Вычислим значения у координат точек пересечения:
у=2х+5
у₁=2(1-2√3/2)+5
у₁=2-4√3/2+5
у₁=7-4√3/2 (≈2,1)
у₂=2(1+2√3/2)+5
у₂=2+4√3/2+5
у₂=7+4√3/2 (≈11,9)
Координаты первой точки пересечения графиков: [(1-2√3/2 (≈ -1,5); 7-4√3/2 (≈2,1)];
Координаты второй точки пересечения графиков: [1+2√3/2 (≈3,5); 7+4√3/2 (≈11,9)]
,
, a 
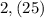
целая часть. У нас она равна 2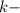
- количество цифр в периоде. У нас их 2
количество цифр до периода. У нас их 0
все цифры, включая период, в виде натурального числа. У нас это 25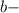
все цифры без периода в виде натурального числа. Их нет.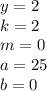
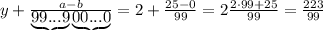
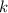подставляется количество 9, а под 
-количество нулей. У нас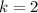 
, значит пишем две цифры 9, а 
, значит, нулей не пишем вообще. Между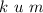 
не стоит знак умножения
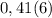
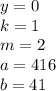
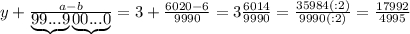
x = (- 1)^n * arcSin1/2 + Пn, n э z
x = (- 1)^n * П/6 + Пn, n э z
Решения уравнения на промежутке (0; 2П) будут П/6, 5П/6, 7П/6, 11П/6