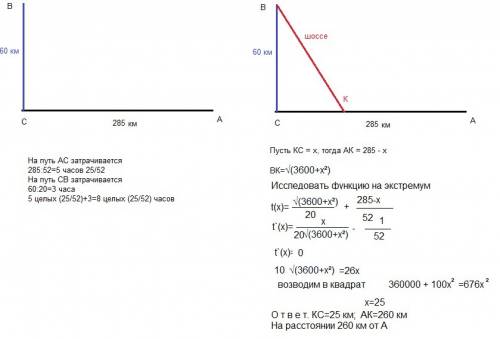
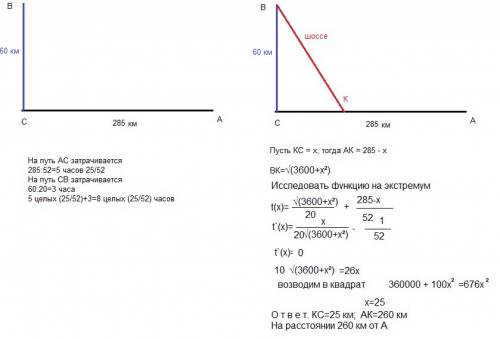
. Любое число можно представить в виде произведения простых множителей. Запишем:
, где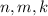 
- некоторые натуральные числа.
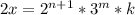является полным квадратом, значит 
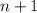и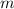 
- четные числа, а 
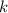- полный квадрат. Аналогично, число 
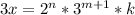является полным кубом, значит 
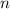и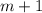 
делятся на 3, а 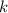- полный куб. 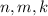это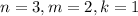 
, значит 
.
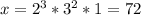Если левая и правая части уравнения являются рациональными выражениями, то такие уравнения называют рациональными.
Рациональные уравнения, в которых и левая и правая части являются целыми выражениями, называются целыми. После упрощения целого уравнения его левая часть представляет собой многочлен.
Например, 2х + 5 = 3(8 - х) - целое, х - 5/х = -3х + 19 - не является целым, оно является дробным.
Степень целого уравнения - это степень многочлена.
Степень многочлена - это степень старшего члена многочлена.
Например, у многочлена х + 5 - степень 1-я, х² + 3х -2 - степень 2-я,
х + 4х² - х³ - 3-я степень.
