1.12m+20m^-60m-20m^=-48m
Дана функция:
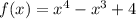
Найдём её производную ( f'(x) = g(x) ):
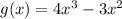
Для поиска и отсеивание экстремумов приравняем производную к нулю:
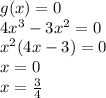
Мы нашли 2 точки возможного экстремума. Проверим, действительно ли они являются точками экстремума. Для этого возьмём по точке в окрестностях этих, и подставим в g(x), чтобы определить знак производной.
1) Подставим в g(x) точку -1, которая < 0:
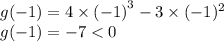
Так как g(-1) < 0, то функция в окрестности точки -1 спадает;
2) Подставим в g(x) точку 0.5, которая лежит между 0 и 3/4:
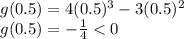
Так как g(0.5) < 0, то функция в окрестности 0.5 спадает;
3) Подставим в g(x) точку 1, которая > 3/4:
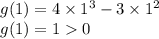
Так как g(1) >0, то функция в окрестности точки 1 возрастает.
Имеем:
На промежутке хє(-∞;0) функция спадает; хє(0;3/4) – функция спадает; хє(3/4;+∞) – функция возрастает. Значит у данной функции существует единственная точка экстремума – 3/4.
Но так как в окрестности точки 3/4 функция производная функции меняет свой знак с "-" на "+", то эта точка является локальным минимумом функции. Тогда локальный максимум функции – 0.
Это и есть ответ.
4m(3+5m)-10m(6+2m)(раскрываем скобки)=12m+20m(m вквадрате)-60m-20m(m вквадрате)=-48m