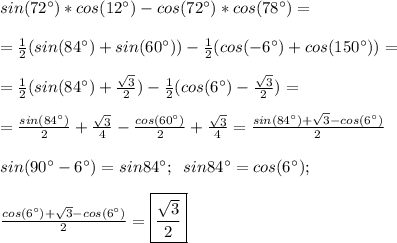
ответ: Сумма внешних углов выпуклого многоугольника равна 360°
Объяснение:
Сумма внешних и внутренних углов любого n-угольника при всех его вершинах равна 180°•n. (т.к. внутренний и внешний угол при одной вершине – смежные и составляют развернутый угол. ) Для нахождения суммы внешних углов из 180°•n вычитается сумма N внутренних углов многоугольника..
Объяснение для 12-угольника.
Сумму внутренних углов выпуклого многоугольника находят по формуле N=180°•(n-2), где N- сумма внутренних углов, n – количество вершин многоугольника. Для треугольника это 180°•(3-2)=180°, для 12-угольника N=180°•(12-2)=1800°.
12•180°= 21600 - сумма всех внутренних и внешних углов 12-угольника, взятых по одному при каждой вершине. Из них на внешние углы приходится 21600°-1800°=360°.
Пусть количество сотен трёхзначного числа равно n,тогда количество десятков этого числа равно n-1, а количество его единиц равно n-2, т.к. по условию задачи цифры трёхзначного числа последовательно уменьшаются. Получим число 100n+10(n-1)+(n-2).
Число, записанное теми же цифрами, но в обратном порядке запишем так: 100(n-2)+10(n-1)+n.
Найдём разность этих чисел:
100n+10(n-1)+(n-2) - (100(n-2)+10(n-1)+n) =
=100n+10(n-1)+(n-2)-100(n-2)-10(n-1)-n=
=99n-99(n-2) = 99n-99n+99*2 =99*2=198
Число 198 делится на 2, т.к. оно чётное (т.е. оканчивается чётной цифрой 2).
Число 198 делится на 9, т.к. сумма его цифр делится на 9 (1+9+8=18).
18:9=2
Число 198 делится на 11, т.к. 9-(1+8)=0 разность числа, стоящего на четном месте и суммы цифр на нечетных местах равна 0 - признак деления на 11. (198:11=18)
Что и требовалось доказать.