x=2
Объяснение:
7^(x) - 5^(x+1) = 3 * 5^(x-1) - 13 * 7^(x-1)
5^(x-1)+7^x -1= 3/25 - 13*5^(-x-1)*7^(x-1)
e^(log5(-x-1)+log7x)-1=3/25 -13e^(log5(-x-1)+log7(x-1))
-28/25 + 13e^(log5(-x-1)+log7(x-1))+e^(log5(-x-1)+log7x)=0
-7^(x-1)+25^(-x-1)(4*7^(2-x)*25^x-4*5^(x+2))=0
7^(x-1)=0; 25^(-x-1)=0; 4*7^(2-x)*25^x-4*5^(x+2)=0
25^(-x-1)=0; 4*7^(2-x)*25^x-4*5^(x+2)=0
4*7^(2-x)*25^x-4*5^(x+2)=0
4(5/7)^x(49*5^x-25*7^x)=0
(5/7)^x(49*5^x-25*7^x)=0
(5/7)^x=0; (49*5^x-25*7^x)=0
49*5^x-25*7^x=0
49*5^x=25*7^x
5^x*7^2=5^2*7^x
x=2; 2=x
x=2


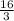
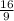
 или х₂ = 1
или х₂ = 1