Проверим.
Найдем функцию, обратную для f(x)
Для этого выразим х через у. у=f(x)
3х=у-5⇒х=у/3-5/3
Заменим х игреком, получим у=х/3-5/3, т.е. функцию g(x)
Да, являются данные в условии функции взаимно обратными.
1. Для первого значения аргумента функция является непрерывной, т.к. подставляя значения аргумента в уравнение получим: 9/2 - это число, слудовательно, условие существования функции соблюдено. Для второго - разрывна, так как знаменатель оюращается в ноль, на ноль делить нельзя в школьной программе.
2. Из последнего предложение следует, что точка 2 - точка разрыва функции, тогда сможем найти лево- и правосторонние пределы: lim x to 2- = 9/ 0- = - бесконечность
lim х to 2+ = 9/0+ = + бесконечность
Нахождение области определения функции
все кроме x=0
Исследование поведения функции на границе области определения
limf(x) при x__0=(4-x^3)/0=+бесконечность
Исследование функции на четность или нечетность
F(-x)=4-(-x)^3/(-X)^2=4+x^3/X^2 функция не является ни четной ни нечетной те общего типа
определить промежутки возрастания и убывания функции
F'(x)=((4-X^3)'*x^2-(X^2)'*(4-x^3))/x^4=-(x^4+4x)/x^4=-(x^3+4)/X^3
стационарная точка (где числитель в нуль) при X=корень кубический из 4
нуль знаменателя это X=0 критическая точка
рисуем координатную прямую ставим на ней точки 0 и корень кубический из 4
определяем знаки в промежутках ,
F'(-2)=-(-4/-8)=-1/2 слева до нуля -
F'(1)=-5/1=-5 от нуля до корня кубического из 4-
F'(2)= -12/8 от кубического корня до -
функция монотонна и убывает
промежутки вогнутости и выпуклости функции
F''(x)=-((x^3+4)'*x^3-(x^3)'*(x+4))/x^6=-3x^3-3/x^4
исследуемые точки x=0 x =-1
ставим их на прямую проверяем промежутки
до -1 знак - функция вогнута
от -1 до 0 знак + функция выгнута
от 0 до + бесконечности - функция вогнута
точка x=-1 точка перегиба
рисуем график
ответ: да.
Найдём функцию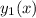
, обратную функции 
.
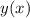Функци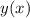и
и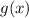 
взаимно-обратные.