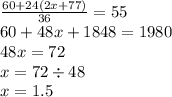
Пусть скорость горной реки х
Плот плывет по реке 21 км в течение 21:х часов
Туристы на лодке все расстояние проплыли за такое же время:
54:(12+х) плыла лодка по реке + 6:12 по озеру и все это равно времени, за которое плот плывет по реке 21 км, =21:х
Составим и решим уравнение:
54:(12+х) +0,5 =21:х
Умножим обе части на х(12+х), чтобы избавиться от дробей:
54х +0,5х(12+х) =21(12+х)
54х +6х +0,5х² =252+21х
0,5х²+39х -252=0
D=b²-4ac=39²-4·0.5·-252=2025
Так как дискриминант больше нуля, то уравнение имеет два корня
Один отрицательный и не подходит ( -84)
Второй = 6
Скорость течения горной реки 6 км/ч
Решение силой Разума - Не допускается деление на ноль.
Решение.
a).
3 - х ≠ 0 или х≠ 3 - первая дробь
(x² - 9) = (x-3)*(x+3) ≠0 х ≠ -3, х ≠ 3 - вторая дробь.
В третьей дроби всегда положительное число.
ОТВЕТ: ОДЗ: х ≠ -3, х≠ 3.
б)
Решаем квадратные уравнения в знаменателях.
x² - 2x - 15 = 0 - уравнение в знаменателе первой дроби.
Находим дискриминант
D = (-2)² - 4*1*(-15) = 64, √64 = 8, корни: x₁ = -3, x₂ = 5.
х² + 8х + 15 = 0 - уравнение в знаменателе второй дроби.
D = 8² - 4*1*15 = 4, √4 = 2, корни: x₃ = -3, x₄ = -5
Значения при которых знаменатель становится равным 0 исключаем из ОДЗ. Значение х = - 3 - общее.
ОТВЕТ: ОДЗ: Х≠ -5 ; Х≠ -3; Х≠ 5
2а) ОДЗ: Х≠ 1 - ответ
2б) ОДЗ: Х≠ 0; Х≠ 3 - ответ.
Объяснение:
ответ: x = 1,5