Кол-во таких чисел=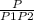 .
.
Здесь P -общее кол0во перестановок 6 чисел : P=6!=60*12
P1 - число перестановок цифры 1 в этом числе. То есть мы как бы путем деления общего числа перестановок на число перестановк конкретной цифры убираем повторяющиеся перестановки, образуемые этой цифрой. Так как кол-во единиц в наборе 2 штуки, то
P1=2!=2
Аналогично для P2=3!=6
P= 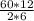 =60.
=60.
если бы например в наборе были бы только единицы напрмиер, то получилось бы единственное возможное число, что доказывает некоторую универсальность моей формулой
3x+4y=-24|*4
12x-9y=36
12x+16y=-96
25y=-132
y=-132/25=-5.28
4x-3y=12
4x-3*(-132/25)=12
100x+396=300
100x=300-396
100x=-96
x=-96/100
x=-0.96
ответ : х=-0.96; у=-132/25=-5.28