![a^3\cdot \sqrt[4]{a}=\sqrt{(a^3)^4\cdot a}=\sqrt[4]{a^{12}\cdot a}=\sqrt[4]{a^{13}}\; \; ,\; \; a0\\\\\\\sqrt[4]{3a^7}=\sqrt[4]{3a^4\cdot a^3}=a\sqrt[4]{3a^3}\; ,\; \; a0\\\\\\\sqrt[5]{-32}+\sqrt[4]{625}+\sqrt[3]{1000}=\sqrt[5]{-2^5}+\sqrt[4]{5^4}+\sqrt[3]{10^3}=-2+5+10=13](/tpl/images/0916/5538/2afab.png)
х мальчиков в классе
у девочек в классе
3х/5 мальчиков изучают английский язык
3у/7 девочек изучают английский язык
2х/5 мальчиков изучают немецкий язык
4у/7 девочек изучают немецкий язык
По условию
(3х/5 + 3у/7) > (2х/5 + 4у/7) на 2
Получаем уравнение:
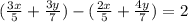
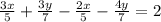

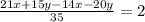


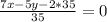
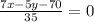
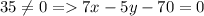
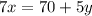
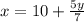
По условию
25 < (x+y) < 36 => (x+y) ∈ (25; 36)
Далее решаем методом подбора.
1) Пусть 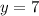 , тогда
, тогда 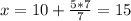
х=15; у=7
(х+у) = 7+15=22 ∉ (25; 36)
2) Пусть  , тогда
, тогда 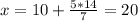
х=20; у=14
(х+у) = 14+20=34 ∈ (25; 36)
Получаем:
20 мальчиков в классе
14 девочек в классе
20-14 = 6
В классе на 6 мальчиков больше, чем девочек.
ответ под буквой А. Мальчиков, на 6.
х мальчиков в классе
у девочек в классе
3х/5 мальчиков изучают английский язык
3у/7 девочек изучают английский язык
2х/5 мальчиков изучают немецкий язык
4у/7 девочек изучают немецкий язык
По условию
(3х/5 + 3у/7) > (2х/5 + 4у/7) на 2
Получаем уравнение:
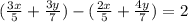
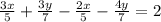

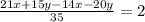


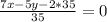
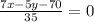
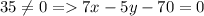
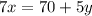
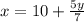
По условию
25 < (x+y) < 36 => (x+y) ∈ (25; 36)
Далее решаем методом подбора.
1) Пусть 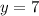 , тогда
, тогда 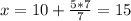
х=15; у=7
(х+у) = 7+15=22 ∉ (25; 36)
2) Пусть  , тогда
, тогда 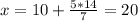
х=20; у=14
(х+у) = 14+20=34 ∈ (25; 36)
Получаем:
20 мальчиков в классе
14 девочек в классе
20-14 = 6
В классе на 6 мальчиков больше, чем девочек.
ответ под буквой А. Мальчиков, на 6.
ответ: решение смотри на фотографии
Объяснение: