x2 + 4x + 8 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 42 - 4·1·8 = 16 - 32 = -16
Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
4x2 - 12x + 9 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-12)2 - 4·4·9 = 144 - 144 = 0
Так как дискриминант равен нулю то, квадратное уравнение имеет один действительных корень:
x = 122·4 = 1.5
3x2 - 4x - 1 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-4)2 - 4·3·(-1) = 16 + 12 = 28
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = 4 - √282·3 = 23 - 13√7 ≈ -0.21525043702153024
x2 = 4 + √282·3 = 23 + 13√7 ≈ 1.5485837703548635
2x2 - 9x + 15 = 0 Найдем дискриминант квадратного уравнения: D = b2 - 4ac = (-9)2 - 4·2·15 = 81 - 120 = -39 Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.В решении.
Объяснение:
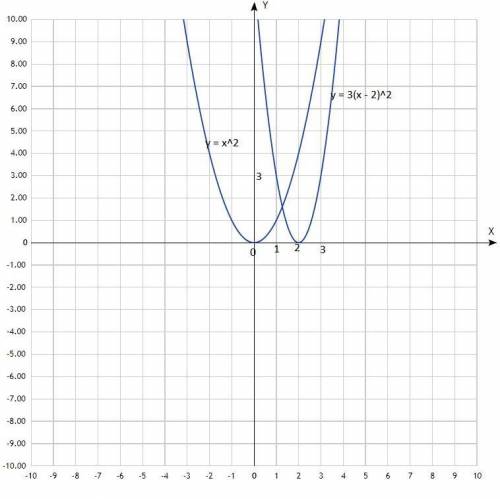
Побудуйте графік функції у = 3(х – 2)2 за до геометричних перетворень. Підготуйте таблицю значень початкової функції у = х2, вибравши зручні для побудови значення аргументу.
Постройте график функции у = 3(х – 2)² с геометрических преобразований. Подготовьте таблицу значений начальной функции
у = х², выбрав удобные для построения значения аргумента.
График функции у = 3(х – 2)² парабола, получен при сдвиге классической параболы у = х² на две единицы вправо и "уже" её за счёт множителя 3.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х 0 1 2 3 4
у 12 3 0 3 12
По вычисленным точкам построить параболу.
Таблица значений начальной функции у = х²:
х -3 -2 -1 0 1 2 3
у 9 4 1 0 1 4 9
D=(2m+1)²-4m²=(2m+1-2m)(2m+1+2m)=4m+1
D≥0
[x₁=(2m+1-√(4m+1))/2
[x₂= (2m+1+√(4m+1))/2
1). D=0 ⇒ m=-1/4
(x-1/4)²>0
x∈R \{1/4}
2). D>0 ⇒ m>-1/4
x₁ < x₂
__+___\x₁x₂/__+__
x∈(-∞; (2m+1-√(4m+1))/2 )∪( (2m+1+√(4m+1))/2 ; ∞)
3). m<-1/4, D<0 ⇒ f(x)>0, x∈R