Объяснение:
Відповідь: правду сказали Андрій та Олеся.
Розв’язання. Позначивши через A, B та O точки, в яких роз-
ташовуються оселі відповідно Андрія, Богдана та Олесі, за-
пишімо висловлювання друзів таким чином:
Андрій: AB AO > 2 .
Богдан: BO AB > 2 .
Олеся: BO AO > 2 .
Якщо справедливими є останні два твердження, то, додавши їх, отримаємо 2 22 BO AB AO > + , або
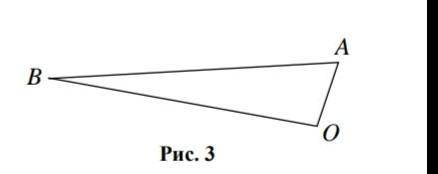
BO AB AO > + , що суперечить нерівності трикутника для точок A, B, O (рис. 3). А якщо справ-
джуються перше та друге твердження, то AB BO AO AB +> + 2 2 ⇒ BO AO AB AO AB > +> + 2 ,
що знову дає суперечність.
З іншого боку, перше й третє твердження справді можуть викону-
ватися водночас, якщо, наприклад, Андрій та Олеся живуть поруч,
а Богдан мешкає дуже далеко від них (як показано на рис. 3).
2) Если f'(x) ≥ 0, функция не убывает данном промежутке, если f'(x) ≤ 0, то не возрастает. Эти промежутки и есть интервалы монотонности.
Вот и все. Рассмотрим Ваш пример:
f(x) = 3x² - 18x + 1.
f'(x) = 6x - 18.
6x - 18 ≥ 0, т.е. x ≥ 3 - функция не убывает.
x ≤ 3 - функция не возрастает.
(Можно также говорить возрастает/убывает, но тогда надо концы интервалов не включаются: например, здесь если x > 3, то функция возрастает. Т.к. на самих концах функция не возрастает/не убывает, эти точки или включаются в оба промежутка, или нет, в зависимости от того, как Вы говорите: не убывает/не возрастает или возрастает/убывает).
ответ: функция не убывает: x ≥ 3, не возрастает: x ≤ 3.
В данном случае с параболой можно было сделать проще. График этой параболы легко представить: это парабола ветвями вверх (a = 3 > 0), значит, до вершины функция убывает, после - возрастает. Ищем вершину: x₀ =
Надеюсь, что Если что, задавайте вопросы в комментарии.