Объяснение:
Для того, чтобы данная последовательность являлась арифметической прогрессией, необходимо и достаточно, чтобы для любого значения n разность между n+1 - м и n - м членами была постоянной. В данном случае yn=36-15n, а y(n+1)=36-15*(n+1)=21-15*, так что y(n+1)-yn=21-15*n-(36-15*n)=-15. Значит, данная последовательность действительно является арифметической прогрессией с разностью d=-15. Её первый член y1=36-15*1=21, а 15-й y15=36-15*15=-189. Так как Sn=n*(y1+yn)/2, то S15=15*(21-189)/2=-1260.
Нам дана квадратичная функция.Ее графиком является парабола.Сначала нам надо узнать где она пересекает ось икс.Для этого приравняем ее к нулю и найдет корни(точки пересечения)
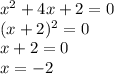
Квадрат в скобке "исчез" тк я понизила степень.Нам дана парабола ветви которой направлены вверх,потому что x^2>0.Если ветви параболы направлены вверх,то промежуток ее возрастания лежит за ее ветвями.Показано на рисунке.А если вниз,то промежуток наоборот внутри.Поэтому промежуток возрастания равен
х>-2 x>-2.Заметем что неравенство у нас строгое ,поэтому -2 в промежуток не входит

тогда:
(u³(v))' = 3u² * u' = 3u² * (sinv)' = 3sin²(x³) * (sinx³)' * (x³)' = 3sin²(x³) * cos(x³) * 3x² = 9sin²(x³) cos(x³) * x²