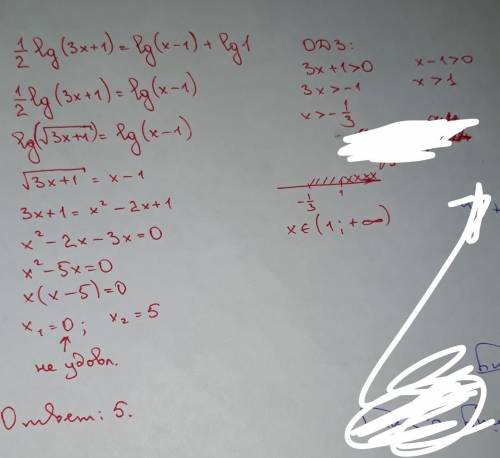
(см. объяснение)
Объяснение:

Наименьшее значение, которое может принимать левая часть рано 8.
Наибольшее значение, которое может принимать правая часть равно 8.
Значит исходное равенство становится верным, если имеем 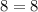 .
.
Тогда перейдем к системе уравнений:

Понятно, что вторая ее строчка решается несложно:
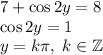
Поработаем теперь с первой:

Введем замену вида  .
.
Тогда уравнение выше можно переписать:
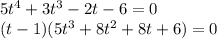
Один из корней очевиден и равен 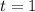 .
.
Понятно, что при  уравнение
уравнение  не имеет корней.
не имеет корней.
Выполним теперь обратную замену:

Тогда ответом будет:

Задание выполнено!