Исходный график:
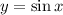
Растягиваем в два раза от оси y. Получим:
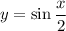
Выполняем симметрию относительно оси y. Получаем:
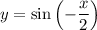
Выполняем сдвиг на п/6 единиц направо. Получаем:
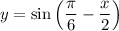
Растягиваем в 2 раза от оси х. Получаем:
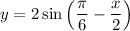
Выполняем симметрию относительно оси y. Получаем:
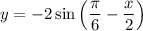
Выполняем сдвиг на 3 единицы вверх. Получаем искомый график:
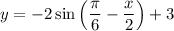
Цепочку рассуждений можно упростить, если воспользоваться нечетностью функции синуса и преобразовать исходную функцию:
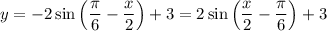
Тогда алгоритм действий будет следующий:
- растяжение в 2 раза от оси x
- сдвиг на п/6 единиц вправо
- растяжение в 2 раза от оси y
- сдвиг на 3 единицы вверх
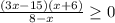
Найдем ОДЗ (Область допустимых значений). Т.к. на ноль делить нельзя, знаменатель не должен быть равен 0. Отсюда находим:
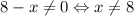
Дальше можно решить разными
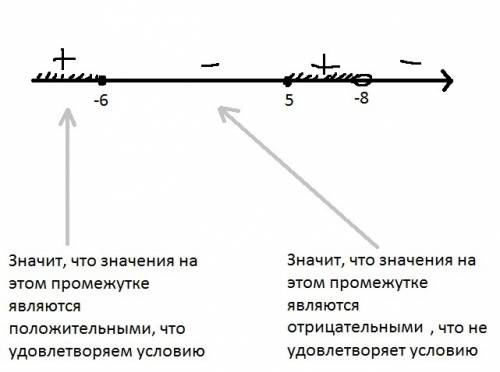
Решим методом интервалов (более удобен):
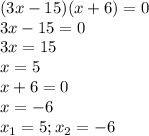
Отмечаем точки ОДЗ и решения на координатной прямой, находим знаки для каждого промежутка и находим решение неравенства (см. прикрепленный рисунок).
P.S. Незакрашенные точки значат, что это значение не входит в промежуток (обозначается круглой скобочкой), а закрашенные - наоборот (обозначается квадратной скобочкой).
![x\in(-\infty;-6]\cup[5;8)](/tpl/images/0942/7912/1fa84.png)
Решим с правила расщепления:
Т.е. существуют два случая, при которых частное 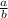 может быть ≥ 0 (Нужно использовать >, < вместо ≥, ≤ соответственно для знаменателя, поскольку он не может быть равен 0):
может быть ≥ 0 (Нужно использовать >, < вместо ≥, ≤ соответственно для знаменателя, поскольку он не может быть равен 0):
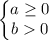 или
или 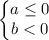
Т.е. решением является совокупность (нас устраивает и то, и другое решение):
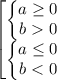
Зная это правило, решаем неравенство:
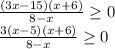
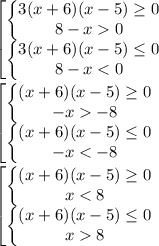
Решим, для удобства, неравенства отдельно.
Первое:
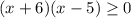
Возможны два случая, когда произведение a × b может быть ≥ 0:
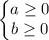 или
или 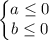
Т.е. решением является совокупность (нас устраивает и то, и другое решение):
![\begin{bmatrix}\left\{\begin{matrix}x+6\geq0\\x-5\geq0\end{matrix}\right.\\\left\{\begin{matrix}x+6\leq0\\x-5\leq0\end{matrix}\right.\end{matrix}\\\\\begin{bmatrix}\left\{\begin{matrix}x\geq-6\\x\geq5\end{matrix}\right.\\\left\{\begin{matrix}x\leq-6\\x\leq5\end{matrix}\right.\end{matrix}\\\\\begin{bmatrix}x\in[5;+\infty)\\x\in(-\infty;-6]\end{matrix}\\x\in(-\infty;-6]\cup[5;+\infty)](/tpl/images/0942/7912/dd8a0.png)
Второе:
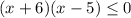
Возможны два случая, когда произведение a × b может быть ≤ 0:
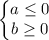 или
или 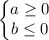
Т.е. решением является совокупность (нас устраивает и то, и другое решение):
![\begin{bmatrix}\left\{\begin{matrix}x+6\leq0\\x-5\geq0\end{matrix}\right.\\\left\{\begin{matrix}x+6\geq0\\x-5\leq0\end{matrix}\right.\end{matrix}\\\\\begin{bmatrix}\left\{\begin{matrix}x\leq-6\\x\geq5\end{matrix}\right.\\\left\{\begin{matrix}x\geq-6\\x\leq5\end{matrix}\right.\end{matrix}\\\\\begin{bmatrix}x\in\O\\x\in[-6;5]\end{matrix}\\x\in[-6;5]](/tpl/images/0942/7912/eb716.png)
Вернемся к решению другой совокупности:
![\begin{bmatrix}\left\{\begin{matrix}(x+6)(x-5)\geq0\\x8\end{matrix}\right.\end{matrix}\\\\\begin{bmatrix}\left\{\begin{matrix}x\in(-\infty;-6]\cup[5;+\infty)\\x\in(-\infty;8)\end{matrix}\right.\\\left\{\begin{matrix}x\in[-6;5]\\x\in(8;+\infty)\end{matrix}\right.\end{matrix}\\\\\begin{bmatrix}x\in(-\infty;-6]\cup[5;8)\\x\in\O\end{matrix}\\\\x\in(-\infty;-6]\cup[5;8)](/tpl/images/0942/7912/144a0.png)
Учитывая ОДЗ, найдем решение:
![\left\{\begin{matrix}x\in(-\infty;-6]\cup[5;8)\\x\neq8\end{matrix}\right.\\x\in(-\infty;-6]\cup[5;8)](/tpl/images/0942/7912/008e1.png)
Теперь решим другое неравенство.
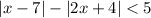
Зная, что 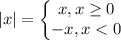 разделим наше неравенство на 4 системы:
разделим наше неравенство на 4 системы:
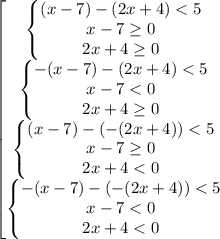
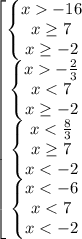
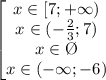
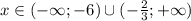
Пусть х км/ч-скорость автом., т-время , которое затратил от А до В.
240/х=т
120/х+120/(х+10)=т-(24/60) Решаем эту систему:
(120/х+120/(х+10)=240/х - 0,4
120/(х+10)-120/х+0,4=0
(120х-120(х+10)+0,4x^2+0,4*(10x)=0, х(х+10)не =0
0,4x^2+4x-1200=0
D1=4+1200*0,4=484=22^2
x1=(-2-22)/0,4=-440/4=-110 не подходит, т.к. скорость больше 0
х2=(-2+22)/0,4=20/0.4=200/4=50
ответ 50км/ч