x-количество квартир в 1 доме, (x+86)-количество квартир во 2 доме. уравнение: x+(x+86)=792; x+x=792-86; 2x=706; x=706/2=353(квартиры)- в 1 доме, 353+86=439(квартиры)-во 2 доме.
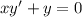
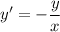 - уравнение с разделяющимися переменными
- уравнение с разделяющимися переменными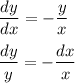
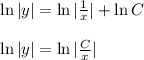
 - общее решение
- общее решение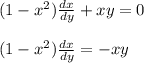

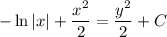 - общий интеграл
- общий интеграл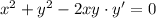

 , тогда
, тогда 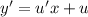



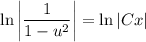
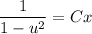
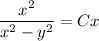 - общий интеграл
- общий интеграл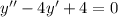
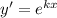 , тогда будем иметь характеристическое уравнение следующего вида:
, тогда будем иметь характеристическое уравнение следующего вида:
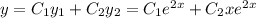 - общее решение
- общее решение
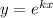 , тогда получаем
, тогда получаем
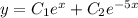

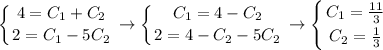
 - частное решение
- частное решение
x+y=792
y+86+y=792
2y=706y
у=353(1 дом)
x=353+86
х=449(2 дом)