Действительных корней нет.
Комплексные корни:
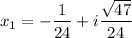
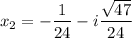
Объяснение:
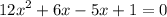
Приводим подобные слагаемые:
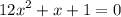
Это обычное квадратное уравнение. Решим через дискриминант.
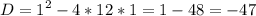
Дискриминант меньше нуля, следовательно действительных корней нет.
Найдем комплексные корни.
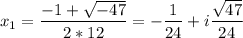
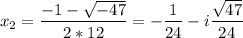
Теория:
Стандартный вид квадратного уравнения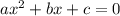 
, 
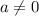
Дискриминант 
Если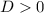 
, то квадратное уравнение имеет два действительных корня.
Если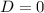 
, то квадратное уравнение имеет один действительных корень.
Если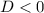 
, то квадратное уравнение не имеет действительных корней, однако комплексные корни существуют.
Комплексное число - число вида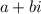 
, где 
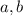- действительные числа, 
- мнимая единица.
Мнимая единица - число, для которого выполняется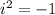 
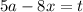, тогда получим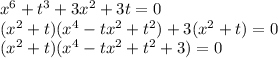 
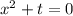
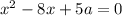
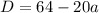
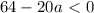
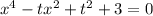
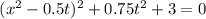
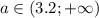
|x²-12x|>x²-12x
Неравенство верно только при
x²-12x<0
x(x-12)<0
x∈(0; 12)