Решить каждую систему двумя методом крамера и методом гаусса) 1) 2)

👇

Увидеть ответ

Ответ:

ShudrenkoArtem

27.11.2022

1 система:

3x-8y=-2

2x+y=5

Перепишем систему уравнений в матричном виде и решим её методом Гаусса

3 -8 I -2

2 1 I 5

1 строку разделим на 3

1 - 8/3 I - 2/3

2 1 I 5

от 2 строки отнимаем 1 строку, умноженную на 2

1 - 8/3 I -2/3

0 19/3 I 19/3

2 строку разделим на 19/3

1 - 8/3 I -2/3

0 1 I 1

к 1 строке добавляем 2 строку, умноженную на 8/3

1 0 I 2

0 1 I 1

x = 2

y = 1

Перепишем систему уравнений в матричном виде и решим её методом Крамера

∆ = I3 -8I

I2 1 I = 19

∆1 = I-2 -8I

I5 1 I = 38

∆2 =I 3 -2I

I2 5I = 19

x = ∆1/∆ = 38/19 = 2

y = ∆2/∆ = 19/19 = 1

2 система:

2x+7y-z=-5

x-5y+2z=0

3x+y-3z=-9

Перепишем систему уравнений в матричном виде и решим её методом Гаусса

2 7 -1 I-5

1 -5 2 I0

3 1 -3 I-9

1 строку делим на 2

1 3.5 -0.5 I-2.5

1 -5 2 I0

3 1 -3 I-9

от 2 строки отнимаем 1 строку, умноженную на 1;

от 3 строки отнимаем 1 строку, умноженную на 3;

1 3.5 -0.5 I-2.5

0 -8.5 2.5 I2.5

0 -9.5 -1.5 I-1.5

2 строку делим на -8.5

1 3.5 -0.5 I-2.5

0 1 - 5/17 I- 5/17

0 -9.5 -1.5 I-1.5

от 1 строки отнимаем 2 строку, умноженную на 3.5;

к 3 строке добавляем 2 строку, умноженную на 9.5;

1 0 9/17 I-25/17

0 1 -5/17 I-5/17

0 0 -73/17 I-73/17

3 строку делим на -73/17

1 0 9/17 I -25/17

0 1 - 5/17 I -5/17

0 0 1 I 1

от 1 строки отнимаем 3 строку, умноженную на 9/17 ;

ко 2 строке добавляем 3 строку, умноженную на 5/17 ;

1 0 0 I -2

0 1 0 I 0

0 0 1 I 1

x= -2

y = 0

z = 1

Перепишем систему уравнений в матричном виде и решим её методом Крамера

∆ = I2 7 -1I

I1 -5 2I

I3 1 -3I = 73

∆1 = I-5 7 -1I

I0 -5 2I

I-9 1 -3I= -146

∆2 = I 2 -5 -1I

I 1 0 2I

I3 -9 -3I = 0

∆3 = I 2 7 -5I

I 1 -5 0I

I3 1 -9I = 73

x = ∆1/∆ = -146/73 = -2

y = ∆2/∆ = 0/73 = 0

z = ∆3/∆ = 73/73 = 1

4,7(63 оценок)

Открыть все ответы

Ответ:

lazyseal1488

27.11.2022

0<у<24, 12<х<24, где х=АВ=ВС, у=АС

Объяснение:

Поскольку треугольник равнобедренный, то две стороны у него равны АВ=ВС. Пусть длина стороны АВ=х, длина стороны АС=у. Тогда периметр треугольника Р=х+х+у или 2х+у=48. Учитывая условие существования треугольника (сумма длин двух любых сторон больше длины третьей стороны), мы также получаем два неравенства 2х>у и х+у>х. Отсюда мы получаем множество решений, где длина основания треугольника может быть больше 0, но меньше 24, а длина бедра от 12 до 24 (не включая граничные значения)

Но я думаю, что какое-то условие Вы нам не дописали. :)

4,6(33 оценок)

Ответ:

shaxrizat1

27.11.2022

выпишем координаты данных векторов:

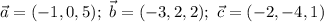
$\vec{a}=(-1,0,5);\ \vec{b}=(-3,2,2);\ \vec{c}=(-2,-4,1)$

координаты:

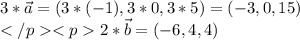
$3*\vec{a}=(3*(-1),3*0,3*5)=(-3,0,15)\\2*\vec{b}=(-6,4,4)$

скалярное произведение векторов - число:

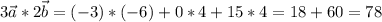
$3\vec{a}*2\vec{b}=(-3)*(-6)+0*4+15*4=18+60=78$

б)

координаты:

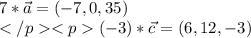
$7*\vec{a}=(-7,0,35)\\(-3)*\vec{c}=(6,12,-3)$

векторное произведение векторов - вектор, находим его координаты:

$7\vec{a}\times (-3\vec{b})=\left|\begin{array}{ccc}\vec{i} & \vec{j} & \vec{k} \\-7 & 0 & 35 \\6 & 12 & -3\end{array}\right|=\vec{i}*\left|\begin{array}{cc}0 & 35 \\12 & -3\end{array}\right|-\vec{j}*\left|\begin{array}{cc}-7 & 35 \\6 & -3\end{array}\right|+\vec{k}*\left|\begin{array}{cc}-7 & 0 \\6 & 12\end{array}\right|=\vec{i}*(-12*35)-\vec{j}*(21-6*35)+\vec{k}*(12*(-7))=\\=-420\vec{i}+189\vec{j}-84*\vec{k}=(-420,189,-84)$

находим модуль(длину) полученного вектора:

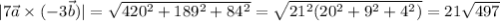
$|7\vec{a}\times (-3\vec{b})|=\sqrt{420^2+189^2+84^2}=\sqrt{21^2(20^2+9^2+4^2)}=21\sqrt{497}$

в)

координаты:

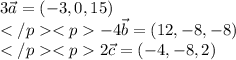
$3\vec{a}=(-3,0,15)\\-4\vec{b}=(12,-8,-8)\\2\vec{c}=(-4,-8,2)$

смешанное произведение векторов - число, находим его:

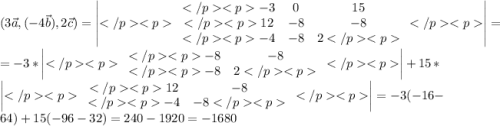
$(3\vec{a},(-4\vec{b}),2\vec{c})=\left|\begin{array}{ccc}-3 & 0 & 15 \\12 & -8 & -8 \\-4 & -8 & 2\end{array}\right|=\\=-3*\left|\begin{array}{cc}-8 & -8 \\-8 & 2\end{array}\right|+15*\left|\begin{array}{cc}12 & -8 \\-4 & -8\end{array}\right|=-3(-16-64)+15(-96-32)=240-1920=-1680$

г)

Координаты:

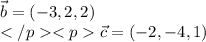
$\vec{b}=(-3,2,2)\\\vec{c}=(-2,-4,1)$

Векторы коллинеарны, если их соответствующие кординаты пропорциональны

Проверим это утверждение:

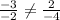
$\frac{-3}{-2}\neq \frac{2}{-4}$

Данное равенство неверно, значит векторы b и c не коллинеарны

Векторы ортогональны, если их скалярное произведение равно нулю.

Проверим это утверждение:

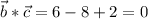
$\vec{b}*\vec{c}=6-8+2=0$

- верно, значит данные векторы ортогональны

Векторы b и c ортогональны

д)

Координаты:

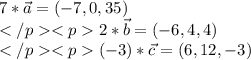
$7*\vec{a}=(-7,0,35)\\2*\vec{b}=(-6,4,4)\\(-3)*\vec{c}=(6,12,-3)$

Три вектора компланарны, если их смешанное произведение равно нулю.

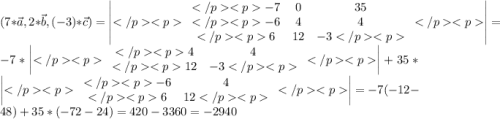
$(7*\vec{a},2*\vec{b},(-3)*\vec{c})=\left|\begin{array}{ccc}-7 & 0 & 35 \\-6 & 4 & 4 \\6 & 12 & -3\end{array}\right|=-7*\left|\begin{array}{cc}4 & 4 \\12 & -3\end{array}\right|+35*\left|\begin{array}{cc}-6 & 4 \\6 & 12\end{array}\right|=-7(-12-48)+35*(-72-24)=420-3360=-2940$