Відповідь:
Пояснення:
# Обидві нерівності рішаємо методом інтервалів .
13) [( x+ 4 )²( x² + 14x + 49 )]/( x + 5 ) ≥ 0 ;
[( x+ 4 )²( x + 7 )²]/( x + 5 ) ≥ 0 ; розглянемо функцію :
f( x ) = [( x+ 4 )²( x + 7 )²]/( x + 5 ) ;
f( x ) = 0 при х = - 7 і х = - 4 ;
f( x ) - невизначена при х = - 5 . Позначимо на числовій осі
f(- 8 ) < 0 ; f(- 6 ) < 0 ; f(- 4,5 ) > 0 ; f( 0 ) > 0 .
x Є {- 7 } U (- 5 ; + ∞ ) .
14) ( 2x + 3 )/( 3 - x ) ≥ ( x + 2 )/( x - 3 ) ;
( x + 2 )/( x - 3 ) + ( 2x + 3 )/( x - 3 ) ≤ 0 ;
( x + 2 + 2x + 3 )/( x - 3 ) ≤ 0 ;
( 3x + 5 )/( x - 3 ) ≤ 0 .
Розглянемо функцію :
f( x ) = ( 3x + 5 )/( x - 3 ) .
f( x ) = 0 при х = - 1 2/3 ;
f( x ) - невизначена при х = 3 . Позначимо на числовій осі
f(- 2 ) > 0 ; f( 0 ) < 0 ; f( 4 ) > 0 .
x Є [- 1 2/3 ; 3 ) .
ответ: 5
Объяснение: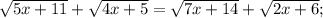 
ОДЗ: 
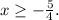
Корень x=5 угадываем (6+5=7+4 - верно). Замена: x+2=p; x=p-2;
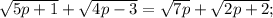
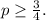Делим уравнение на 
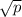и обозначаем 
буквой q; ![q\in (0;\frac{4}{3}]](/tpl/images/4977/5827/f5522.png)
. Получается уравнение
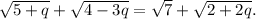Угаданный корень x=5 для исходного уравнения приводит к корню q=1/7 полученного уравнения (подстановка подтверждает это). Докажем, что других корней нет. Для этого с производной убедимся, что левая часть убывает, а правая возрастает. С правой частью всё понятно, разберёмся с левой: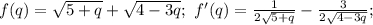 
эта производная равна нулю при 4-3q=9(5+q); 12q=-41; q=-41/12∉(0;4/3]. Поэтому на интервале (0;4/3) производная не меняет знак. Легко убедиться, что этот знак отрицательный, устремив, например, q к 0. Поэтому функция f(q) убывает, а раз функция в правой части уравнения возрастает, другого решения кроме q=1/7 быть не может.
-1_2/3(0.6x-6)-2/3(9x+1.5) = -5/3(3/5 x - 6) - 2/3(9x+1.5) = -x+10-6x-1 = -7x+9
при x=-2,1
-7 * (-2.1) + 9 = 14.7+9 = 23.7