Объяснение:
Квадратное уравнение можно представить в виде:
a(x-x1)(x-x2)=0, где x1 и x2 - корни уравнения;
Раскроем скобки, тогда a*x^2-a*x(x1+x2)+a*x1*x2=0 (1)
у нас выражение x^2-x-p=0 (2)
Если сравнить 2 выражения.
Коэффициент в (2) перед x^2=1, отсюда следует, что в (1) a=1.
(1) принимает вид:
x^2-x*(x1+x2)+x1*x2=0
Сравниваем коэффициенты перед x, получаем
x1+x2=1 (3)
сравниваем свободные члены
-p=x1*x2 (4)
также по условию
x1^2+x2^2=25; (5)
тут 2 варианта, решить систему выше или можно предположить решение;
Предположим, что x1=-4, x2=5;
Тогда удовлетворяются все уравнения условия - (3), (5);
получаем, что p=-(-4)*(5)=20
Если не учитывать, что 100% тоже больше 94%, то:
Пусть х - число домов в этом районе, а х-1 - число домов, имеющих больше 5 этажей
(чтобы найти минимально значение х, разница между числом домов, имеющих больше 5 этажей, и общим числом домов должна быть минимальна)
Получаем уравнение: 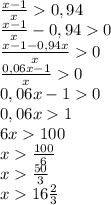
Проверка подбором
11 домов имеют больше 5 этажей
12 домов всего
11 / 12 = 0,91(6) = 91,(6)%
Не подходит.
...
15 домов имеют больше 5 этажей
16 домов всего
15 / 16 = 0,9375 = 93,75%
Не подходит.
16 домов имеют больше 5 этажей
17 домов всего
16 / 17 = 0,941176... = 94,1176...%
Подходит.
ответ: 17 - наименьшее число домов в данном районе.
x²-25y²=(x-5y)(x+5y) x²-10xy+25y²=(x-5y)²
(x-5y)(x+5y)/(x-5y)² это выражение мы можем сократить на (х-5у). Тогда получим ответ (х+5у)/(х-5у)
теперь подставим в эту дробь вместо х 2,6, а вместо у -1,48. получим:
(2,6+5*(-1,48))/(2,6-5*(-1,48))=(2,6-7,4)/(2,6+7,4)=-4,8/10=-0,48
Подробнее - на -