1. Для первого значения аргумента функция является непрерывной, т.к. подставляя значения аргумента в уравнение получим: 9/2 - это число, слудовательно, условие существования функции соблюдено. Для второго - разрывна, так как знаменатель оюращается в ноль, на ноль делить нельзя в школьной программе.
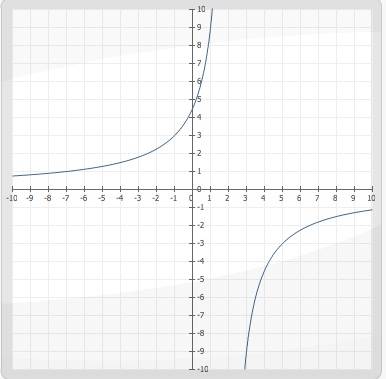
2. Из последнего предложение следует, что точка 2 - точка разрыва функции, тогда сможем найти лево- и правосторонние пределы: lim x to 2- = 9/ 0- = - бесконечность
lim х to 2+ = 9/0+ = + бесконечность
x⁴-x³-3x²+4x-4=x⁴+x³-x²+2x-2x³-2x²+2x-4 = x(x³+x²-x+2)-2(x³+x²-x+2)=(x-2)(x³+x²-x+2) = (x-2)(x³-x²+x+2x²-2x+2)= (x-2)(x(x²-x+1)+2(x²-x+1)) = (x-2)(x+2)(x²-x+1)+2(x²-x+1)
Получили (x-2)(x+2)(x²-x+1)+2(x²-x+1)=0
x²-x+1=0 решения не имеет (D=1-4=-3 <0)
ответ: x₁=-2, x₂=-2