Обратную матрицу найдем по формуле:
,
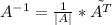где |A| - определитель матрицы, а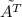 
- транспонированная матрица алгебраических дополнений
![|A|=\left[\begin{array}{ccc}2&3&-1\\1&-1&3\\3&5&1\end{array}\right]=-2+27-5-3-30-3=-16](/tpl/images/0977/0676/37fc7.png)
Т.к. определитель матрицы не равен 0, то обратная матрица существует.
Находим матрицу миноров. Для каждого элемента матрицы соответствующий ему минор вычисляется по определителю матрицы 2х2, которая получается вычеркиванием соответствующей строки и столбца для этого элемента:
![m_{11}=\left[\begin{array}{cc}-1&3\\5&1\end{array}\right]=-1-15=-16\\m_{12}=\left[\begin{array}{cc}1&3\\3&1\end{array}\right]=1-9=-8\\m_{13}=\left[\begin{array}{cc}1&-1\\3&5\end{array}\right]=5+3=8](/tpl/images/0977/0676/87821.png)
![m_{21}=\left[\begin{array}{cc}3&-1\\5&1\end{array}\right]=3+5=8\\m_{22}=\left[\begin{array}{cc}2&-1\\3&1\end{array}\right]=2+3=5\\m_{23}=\left[\begin{array}{cc}2&3\\3&5\end{array}\right]=10-9=1](/tpl/images/0977/0676/4f39c.png)
![m_{31}=\left[\begin{array}{cc}3&-1\\-1&3\end{array}\right]=9-1=8\\m_{32}=\left[\begin{array}{cc}2&-1\\1&3\end{array}\right]=6+1=7\\m_{33}=\left[\begin{array}{cc}2&3\\1&-1\end{array}\right]=-2-3=-5](/tpl/images/0977/0676/280fc.png)
Получили следующую матрицу миноров:
![M=\left[\begin{array}{ccc}-16&-8&8\\8&5&1\\8&7&-5\end{array}\right]](/tpl/images/0977/0676/aa9d0.png)
Из матрицы миноров получим матрицу алгебраических дополнений заменой знака на противоположный у элементов матрицы миноров, у которых сумма номеров строк и столбца нечетна:
![\tilde{A}=\left[\begin{array}{ccc}-16&8&8\\-8&5&-1\\8&-7&-5\end{array}\right]](/tpl/images/0977/0676/69926.png)
Следующим шагом получаем транспонированную матрицу алгебраических дополнений:
![\tilde{A^T}=\left[\begin{array}{ccc}-16&-8&8\\8&5&-7\\8&-1&-5\end{array}\right]](/tpl/images/0977/0676/ab445.png)
Обратная матрица:
![A^{-1}=-\frac{1}{16}\left[\begin{array}{ccc}-16&-8&8\\8&5&-7\\8&-1&-5\end{array}\right]](/tpl/images/0977/0676/543eb.png)
Проверим, что произведение исходной и обратной матрицы равно единичной:
![A*A^{-1}=-\frac{1}{16}\left[\begin{array}{ccc}2&3&-1\\1&-1&3\\3&5&1\end{array}\right]\left[\begin{array}{ccc}-16&-8&8\\8&5&-7\\8&-1&-5\end{array}\right]=-\frac{1}{16}*\left[\begin{array}{ccc}-16&0&0\\0&-16&0\\0&0&-16\end{array}\right]=\left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right]](/tpl/images/0977/0676/51b23.png)
Запишем уравнение кривой в виде -4*(x²-4*x)+25*(y²+4*y)-16=0, или -4*[(x-2)²-4]+25*[(y+2)²-4]-16=0, или -4*(x-2)²+25*(y+2)²=100, или -(x-2)²/25+(y+2)²/4=1. Это есть уравнение гиперболы с центром симметрии в точке (2;-2), вещественной полуосью a=√25=5 и мнимой полуосью b=√4=2. Вершины гиперболы в данном случае лежат на прямой x=2, параллельной оси ординат. Одни из вершин имеет координаты (2;3), другая - координаты (2;-7). Асимптоты гиперболы задаются уравнениями y-y0=b/a*(x-x0) и y-y0=-b/a*(x-x0), где x0 и y0 - координаты центра симметрии. В нашем случае x0=2, y0=-2, a=5,b=2, поэтому уравнения асимптот принимают вид: y+2=2/5*(x-2) и y+2=-2/5*(x-2).
это ж совсем элементарно :)
9/10=0,9 дм
6ч*60+42=402 мин