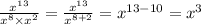
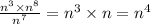
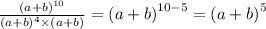
а)(53+27)²=80²=6 400
б)(186-76)²=110²=12 100
в)735²+2·735·728+728²-4·735·728=
=735²-2·735·728+728²=(735-728)²=7²=49
г) (744-740)²=4²=16
д)(306+694)²=1 000²=1 000 000
е)(914+586)²=1500²=2 250 000
ж) (257-143)·(257+143)=114·400=45 600
з)(167-67)·(167+67)=100·234=23 400
и)(162-161)·(162+161):323=1·323:323=1
к)(132-131)(132+131):265=1
л)584+583²-584²+583=
=584+(583²+583)-584²=
=584+583·(583+1)-584²=
=584+583·584-584²=
=584·(1+583-584)=
=584·0=0
м)675+674²-675²+674=675+674²+674-675²=
=675+674·(674+1)-675²=
=675+674·675-675²=
=675·(1+674-675)=
=675·0=0
Відповідь:
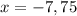
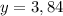
Пояснення:
Перетворимо рівняння системи. Обидві частини першого рівняння системи помножимо на 10, а друге - на 12, отримаємо наступну систему рівняння: 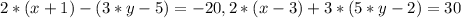
Розкриємо дужки:
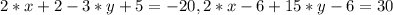
Зведемо подібні доданки в лівих частинах обох рівнянь системи, отримаємо:
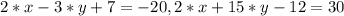
Значення зі змінної залишаємо в лівій частині, а вільні числа переносимо до правої частини, змінюючи знак на протилежний:
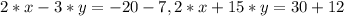
Виконуємо алгебраїчні обчислення в правих частинах обох рівнянь системи:
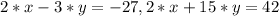
Помножимо обидві частини першого рівняння на 5, отримаємо рівняння:
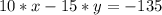
Використовуючи метод додавання, додамо обидві рівняння системи між собою, отримаємо:
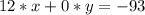
Знаходимо змінну  :
:
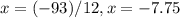
Підставимо змінну  у будь-яке рівняння системи та знайдемо змінну
у будь-яке рівняння системи та знайдемо змінну 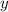 , отримаємо:
, отримаємо:
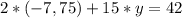
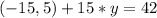
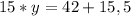
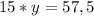
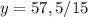
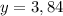
б)n^3*n^1=n^4
(a+b)^10:(a+b)^5=(a+b)^5