
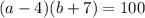


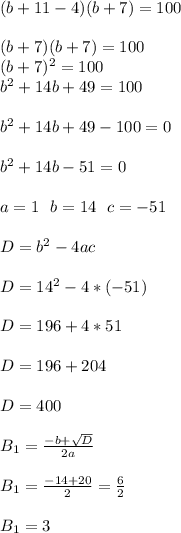
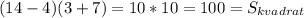
0<у<24, 12<х<24, где х=АВ=ВС, у=АС
Объяснение:
Поскольку треугольник равнобедренный, то две стороны у него равны АВ=ВС. Пусть длина стороны АВ=х, длина стороны АС=у. Тогда периметр треугольника Р=х+х+у или 2х+у=48. Учитывая условие существования треугольника (сумма длин двух любых сторон больше длины третьей стороны), мы также получаем два неравенства 2х>у и х+у>х. Отсюда мы получаем множество решений, где длина основания треугольника может быть больше 0, но меньше 24, а длина бедра от 12 до 24 (не включая граничные значения)
Но я думаю, что какое-то условие Вы нам не дописали. :)
1) 7(x + 1) - 2(x - 4) = x - 9
7x + 7 - 2x + 8 = x - 9
5x - x = - 9 - 15
4x = - 24
x = - 6
2) 3(x - 1) - 2(x - 5) = 5x + 13
3x - 3 - 2x + 10 = 5x + 13
x - 5x = 13 - 7
- 4x = 6
x = - 1,5
3) 2 = (3x - 5) - (7 - 4x)
2 = 3x - 5 - 7 + 4x
2 = 7x - 12
7x = 2 + 12
7x = 14
x = 2