А1) 2
А2) 4 координатная четверть
Объяснение:
А1) Мы можем подставить все значения аргумента для каждого вариант ответа в функцию, и убедится, что y(1) дает наименьшее значение из предложенных. Также можно посмотреть на выражение в функции 2-5x. Если выбирать отрицательный аргумент, то мы только прибавим к 2 некоторое число. Если выбрать как аргумент 0, то останется y=2. А вот если выбрать положительный аргумент, то мы из двойки будем вычитать какое-либо число, что и даст нам наименьшее значение. Положительный аргумент тут у одного вариант ответа: y(1)
А2) Абсцисса положительна, а ордината отрицательна. Это правая нижняя координатная четверть, то есть четвертая.
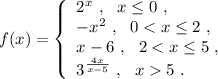
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .
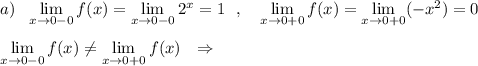
При х=0 функция имеет разрыв 1 рода .
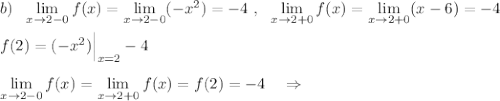
При х=2 функция непрерывна.
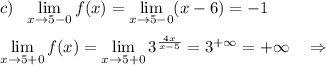
При х=5 функция имеет разрыв 2 рода .
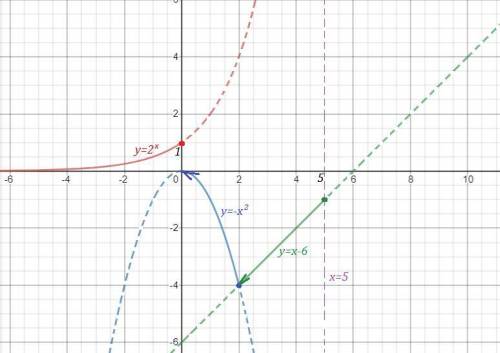
График функции нарисован сплошной линией.
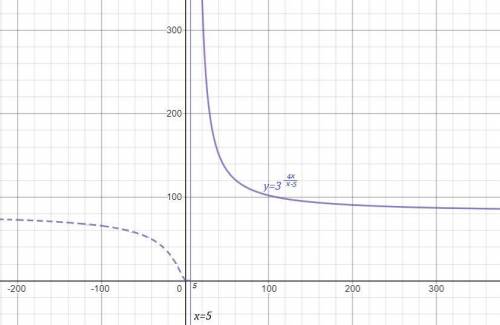
На 1 рисунке нет чертежа функции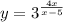 
при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .
перенесем все в левую часть и поменяем знаки
2x^2+3x-3-7x-13=0
2x^2-4x-16=0
D=4^2-2*1*(-8)=36 >0 два корня
x1=(2-6)/2=-2
x2=(2+6)/2=4
наибольший 4