Это квадратное уравнение имеет смысл только тогда когда D=b^2-4*a*c=0, поэтому:
(р + 2)х2 + (р + 2)х + 2 = 0
a=p+2
b=p+2
c=2
D=b^2-4*a*c=0
D=(p+2)^2-4*2*(p+2)=0
(p+2)^2-4*2*(p+2)=0
(p^2+4p+4)-8p-16=0
p^2+4p+4-8p-16=0
p^2-4p-12
D=16+48=64
p1=6 ; p2=-2
ответ: p=6; p=-2.
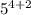 =
=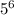
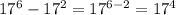
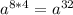
1)Рассм. прямоугольный треуг-к АВD, образованный одной из диагоналей и 2 сторонами прямоугольника(а - первая сторона, b - вторая сторона). Тогда по теореме пифагора квадрат гипотенузы равен сумме квадратов катетов:
45^2 = a^2 + b^2
Площадь прямоугольника - это произведение сторон а и b:
a * b = 972
a^2 + b^2 можно представить как полный квадрат:
(a + b)^2 - 2ab = a^2 + b^2 (a^2 + b^2 + 2ab) - 2ab = a^2 + b^2
2)Теперь вместо ab подставляем 972, вместо a^2 + b^2 - 45^2 (или 2025)
(a + b)^2 - 1944 = 2025
(a + b)^2 = 3989
a + b = кв. корень 3969 = 63
3)Теперь решим систему нера-в:
a + b = 63
a * b = 972, выражаем а через 1-ое урав-е и подставляем во второе:
a = 63 - b
(63 - b) * b = 972
a = 63 - b
63b - b^2 - 972 = 0
a = 63 - b
(b - 27) * (b - 36) = 0 , (следовательно 27 и 36 - корни кв. урав-я),
а = 36 a = 27
b = 27, b = 36, следовательно
27 см и 36 см - длины сторон прямоугольника.
ответ: 27 и 36
(p+2)²-4(p+2)*2=0
p²+4p+4-8p-16=0
p²-4p-12=0
p²-6p+2p-12=0
p(p-6)+2(p-6)=0
(p+2)(p-6)=0
p=-2 ∨ p=6