ответ: дедушке 76 лет, папе 38 лет.
Объяснение: Пусть x лет дедушке, тогда папе x/2 лет. Папе и дедушке вместе 114 лет. Составим и решим уравнение:
x + x/2 = 114 ; 2x + x = 228 ; 3x = 228 ; x = 228/3 ; x = 76
Итак, если дедушке 76 лет, то папе 76/2 = 38 лет.
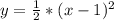
a=x
b=x+7
c=13
c^2=a^2+b^2
169=x^2+x^2+14x+49
120=2x^2+14x
60=x^2+7x
x^2+7x-60=0
D=49+240=289
D=17^2
x1=-7+17/2=5
x2=-12
3.
x - первый катет
y - второй катет
Составляем систему:
x+y =23 (1)
x^2+y^2 = 17^2 (2)
Из первого выражаем, к примеру, х
х=23 - y
Подставляем х в (2)
(23-y)^2 + y^2 = 17^2
529 - 46*y + y^2 + y^2 = 289
2*y^2 - 46*y + 240 = 0
D= 2116 - 1920 = 196 = 14^2
y1=(46+14)/4 =15
y2 = (46-14)/4 = 8
y1=15 x1=8
y2=8 x2=15
Значит катеты равны 8 и 15
Пусть папе х лет, тогда дедушке (2х) лет. Т.к. вместе им 114 лет, то составим и решим уравнение:
х + 2х = 114,
3х = 114,
х = 114 : 3,
х = 38.
Значит, папе 38 лет, а дедушке 38 · 2 = 76 (л.).
ответ: 38 лет и 76 лет.