a=4
(2;1)
Объяснение:
Из условия известно, что первое уравнение этой системы обращается в верное равенство при x= 8 и y= −7; тогда, подставив эти значения переменных в первое уравнение, можно найти коэффициент a.
Получим:
ax+3y=11;8a+3⋅(−7)=11;8a=11−(−21);8a=32;a=4.
При таком значении коэффициента a данная система примет вид:
{4x+3y=115x+2y=12
Для решения этой системы уравнений графически построим в одной координатной плоскости графики каждого из уравнений.
Графиком уравнения 4x+3y=11 является прямая.
Найдём две пары значений переменных x и y, удовлетворяющих этому уравнению.
x −1 2
y 5 1
Построим на координатной плоскости xОy прямую m, проходящую через эти две точки.
Графиком уравнения 5x+2y=12 также является прямая.
Найдём две пары значений переменных x и y, удовлетворяющих этому уравнению.
x 0 2
y 6 1
Построим на координатной плоскости xОy прямую n, проходящую через эти две точки.
Получим:
Прямые m и n пересекаются в точке A, координаты которой являются решением системы, т. е. A(2;1)
Объяснение:
Давайте для начала формализуем условие. У насть есть вероятностное простравнство Ω. Что такое в нём исход? Исход - это как раз передача сообщения n раз. Исход можно закодировать последовательностью n+1 чисел. Каждое число в последовательности обозначает жителя, а следующее жителя которому будет передано сообщение. Получаем, что:
Из условия следует, что каждый исход равновероятен.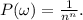
Теперь посчитаем вероятность, что новость будет передана n раз без повторного сообщения её кому-нибудь. Обозначим это событие как A. Заметим, что каждый благоприятный исход (лежит в А) представляет собой перестановку (n+1)-го чисел. Всего таких перестановок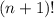
. Теперь можно считать вероятность: