ОДЗ:
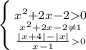
Решаем каждое неравенство:
 ⇒
⇒ 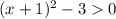 ⇒
⇒

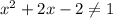 ⇒
⇒  ⇒
⇒ 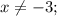
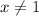

Подмодульные выражения обращаются в 0 в точках
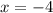 и
и 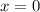
Это точки делят числовую прямую на три промежутка.
Раскрываем знак модуля на промежутках:
(-∞;-4]
|x+4|=-x-4
|x|=-x
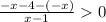 ⇒
⇒  ⇒ x < 1
⇒ x < 1
решение неравенства (-∞;-4]
(-4;0]
|x+4|=x+4
|x|=-x
 ⇒
⇒  ⇒ x < -2 или x > 1
⇒ x < -2 или x > 1
решение неравенства (-4;-2)
(0;+∞)
|x+4|=x+4
|x|=x
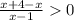 ⇒
⇒  ⇒ x > 1
⇒ x > 1
решение неравенства (1;+∞]
Объединяем ответы трех случаев:
 при
при 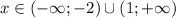
ОДЗ:

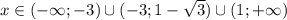
Решаем неравенство: 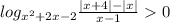
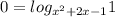
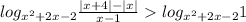
Два случая:
если основание логарифмической функции >1, то она возрастает и большему значению функции соответствует большее значение аргумента
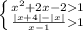 ⇒
⇒  ⇒
⇒ ![\left \{ {{x\in (-\infty;-3) \cup(1;+\infty)} \atop {x\in(-\infty;-4]\cup(1;5)}} \right.](/tpl/images/1360/8793/82812.png)
второе неравенство решаем на промежутках так:
(-∞;-4]
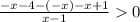 ⇒
⇒  ⇒
⇒ 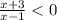 ⇒ (-3;-1)
⇒ (-3;-1)
не принадлежат (-∞;-4]
на (-4;0]
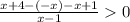 ⇒
⇒ 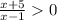 ⇒ x < -5 или x > 1
⇒ x < -5 или x > 1
не принадлежат (-4;0]
(0;+∞)
 ⇒
⇒ 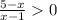 ⇒
⇒ 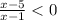 ⇒
⇒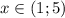
о т в е т этого случая 
если основание логарифмической функции 0 < a < 1, то она убывает и большему значению функции соответствует меньшее значение аргумента
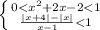 ⇒
⇒  ⇒
⇒ ![\left \{ {{x\in (-3;-1-\sqrt{3}) \cup(-1+\sqrt{3};1)} \atop {x\in(-\infty;-4]\cup(-4;0]\cup(5;+\infty)}} \right.](/tpl/images/1360/8793/ac205.png)
второе неравенство решаем на промежутках так:
(-∞;-4]
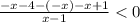 ⇒
⇒ 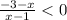 ⇒
⇒ 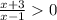 ⇒
⇒
(-∞;-3)U(1;+∞)
о т в е т. (-∞;-4]
на (-4;0]
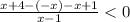 ⇒
⇒ 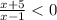 ⇒ -5 < x < 1
⇒ -5 < x < 1
о т в е т. (-4;0]
(0;+∞)
 ⇒
⇒ 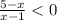 ⇒
⇒ 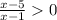 ⇒
⇒
о т в е т этого случая 
С учетом ОДЗ получаем окончательный ответ: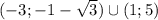
а) 330
б)
в)
Объяснение:
Буду объяснять каждое задание по отдельности. , Согласен, предыдущие выкладки были неправильными. В силу недопонимания во мною, либо двоякостью постановки во Число сочетаний из x по n равно биномиальному коэффициенту
Сₓⁿ= знак равенства не очень ровно размещён относительно дроби.
5 студентов хотят ехать снизу, а 4 сверху. Размещаем их по пожеланию.
a) Если порядок размещения пассажиров как снизу, так и сверху не учитывается то нет их перестановок.
Разместив пятерых студентов снизу и четырёх сверху имеем 7 свободных мест на верхних и 4 на нижних полках. Далее, нужно разместить 11 студентов с расчётом того что не учитываем их перестановок. Значит кол-во комбинаций равно С₁₁⁷·С₄⁴==8·9·10·11÷(1·2·3·4)=330
Аналогично получим С₁₁⁴С₇⁷=330
С₄⁴ здесь не обязательно. Оставим его для определённости последующих решений.