Так как сумма чисел в вершинах есть нечетное число, то как минимум одно число в вершине - нечетное. Получить нечетное число можно лишь перемножая нечетные числа.
Пусть в вершине В нечетное число, тогда на сторонах АВ и ВС нечетные числа.
Чтобы общая сумма чисел в вершинах была нечетной, необходимо оставшиеся три числа взять четными или одно взять четным, а два других нечетными. Но если предположить, что еще хотя бы одно число в вершине нечетное, то по цепочке получим и на следующей стороне нечетное число и после следующего предположения, что в следующей вершине нечетное число (ведь нам нужно два нечетных числа в сумму), на последней стороне получим тоже нечетное число, что будет означать, что и в последней вершине нечетное число. Тогда сумма чисел в вершинах будет четная. Противоречие.
Значит, среди чисел в вершинах только одно нечетное.
По этой расстановке однозначно расставляются числа на сторонах: на двух смежных сторонах - нечетные числа, на двух других смежных сторонах - четные числа.
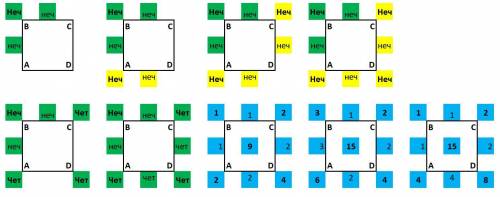
Проверим наименьший вариант: 1, 1, 2, 2:
1·1+1·2+2·2+2·1=1+2+4+2=9
Возьмем вместо одного из чисел следующее за ним по четности, например вместо 1 возьмем 3:
3·1+1·2+2·2+2·3=3+2+4+6=15
сумма чисел на сторонах 3+1+2+2=8
Можно было взять, например, 4 вместо 2:
1·1+1·2+2·4+4·1=1+2+8+4=15
По-прежнему, сумма чисел на сторонах 1+1+2+4=8
Если числа продолжить как-либо увеличивать, то слагаемые в произведении увеличатся, а соответственно и произведение увеличится и не будет равно 15.
ответ: 8
а)y= x² - 4x +3
Уравнение параболы cо смещённым центром, ветви параболы направлены вверх.
A)Найти координаты вершины параболы:
х₀ = -b/2a = 4/2 = 2
y₀ = 2²-4*2 + 3 = 4 - 8 + 3 = -1
Координаты вершины (2; -1)
B)Найти точки пересечения параболы с осью Х, нули функции:
y= x² - 4x + 3
x² - 4x + 3 = 0, квадратное уравнение, ищем корни:
х₁,₂ = (4±√16 -12)/2
х₁,₂ = (4±√4)/2
х₁,₂ = (4±2)/2
х₁ = 1
х₂ = 3
Координаты нулей функции (1; 0) (3; 0)
C)Найти точки пересечения графика функции с осью ОУ.
Нужно придать х значение 0: y = -0+0+3= 3
Также такой точкой является свободный член уравнения c = 3
Координата точки пересечения (0; 3)
Д)Ось симметрии = -b/2a X = 4/2 = 2
Е)Для построения графика нужно найти ещё несколько
дополнительных точек:
х= -2 у= 15 ( -2; 15)
х= 0 у= 3 (0; 3)
х= 6 у= 15 (6; 15)
Координаты вершины параболы (2; -1)
Координаты точек пересечения параболы с осью Х: (1; 0) (3; 0)
Координаты дополнительных точек: ( -2; 15) (0; 3) (6; 15)
При найденных точек можно построить график параболы.
в)у=4х² - 4х -1
Уравнение параболы cо смещённым центром, ветви параболы направлены вверх.
A)Найти координаты вершины параболы:
х₀ = -b/2a = 4/8 = 0,5
y₀ = 4 *0,5²-4*0,5 - 1 = 1 - 2 - 1= -2
Координаты вершины (0,5; -2)
B)Найти точки пересечения параболы с осью Х, нули функции:
y= 4x² - 4x - 1
4x² - 4x - 1 = 0, квадратное уравнение, ищем корни:
х₁,₂ = (4±√16 +16)/8
х₁,₂ = (4±√32)/8
х₁,₂ = (4±5,7)/8
х₁ = 0,21
х₂ = 1,21
Координаты нулей функции (0,21; 0) (1,21; 0)
C)Найти точки пересечения графика функции с осью ОУ.
Нужно придать х значение 0: y = -0+0 -1= -1
Также такой точкой является свободный член уравнения c = -1
Координата точки пересечения (0; -1)
Д)Ось симметрии = -b/2a X = 4/8 = 0,5
Е)Для построения графика нужно найти ещё несколько
дополнительных точек:
х= -2 у= 23 (-2; 23)
х= -1 у=7 (-1; 7)
х= 0 у= -1 (0; -1)
х= 1 у= -1 (1; -1)
х= 2 у= 7 (2; 7)
х= 3 у= 23 (3; 23)
Координаты вершины параболы (0,5; -2)
Координаты точек пересечения параболы с осью Х: (0,21; 0) (1,21; 0)
Координаты дополнительных точек: (-2; 23) (-1; 7) (0; -1) (1; -1) (2; 7) (3; 23)
При найденных точек можно построить график параболы.
4x(y-3)-7(y-3) = (y-3)*(4x-7)