я подозреваю что тут закралась неясность, в прогрессии насколько я помню количество элементов бесконечно, хотя в убывающей геометрической прогресии сумма всех элементов может сходиться.
инфми словами условие следует понимать так что n первых членов прогресии, где n = 2k,
выполняется условие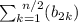 
в три раза больше, чем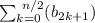 
рассмотрим это более подробно на примере первых шести элементов
сумма нечетных S(1,3,5) = b1 + b3 + b5
сумма четных S(2,4,6) = b2 + b4 + b6 = b1*q + b3*q + b5*q = q(b1 + b3 + b5) = q*S(1,3,5)
следовательно отношение между четной суммой и нечетной равно знаменателю прогрессии.
Для нашей задачи это число 3
ответ 3
3
Ученик каменщика за 1 час укладывает x кирпичей, тогда за 2 часа он укладывает 2x кирпичей .
Каменщик за 1 час укладывает в 6 раз больше кирпичей, чем его ученик, то есть 6x кирпичей, тогда за 6 часов он укладывает 6 * 6x = 36x кирпичей . В результате каменщик уложил на 440 кирпичей больше, чем его ученик. Составим уравнение:
36x-2x=340 ... 34x=340 ... x=10 кирпичей - укладывает ученик каменщика в час.
4
в корзине было х кг винограда, а в ящике 2х кг. после того, как в корзину добавили 2кг, в ней стало х+2 кг винограда, что на 0,5кг больше, чем в ящике.
х+2=2х+0,5
-х=-1,5
х=1,5
в корзине было 1,5кг винограда.
Нужно заучить таблицу квадратов, хотя бы до 20^2 = 400, и извлекать корни.
1) √(16*25) = √16*√25 = 4*5 =. 20
2) √216 = √(36*6) = 6√6
3) 2√14 = √(2^2*14) = √(4*14) = √56
4) 6+ 4√2 = 4+ 4√2+ 2. = 2^2+ 2*2*√2+ (√2)^2 = (2+ √2)^2
5) 26 -15√3 = 8 +18 - 12√3 -3√3 = 2^3 - 3*2^2*√3 + 3*2*(√3)^2 - (√3)^3 = (2-√3)^3
6) (√2-1)*√(3-2√2) + 2√2 = (√2-1)*√(2-2√2+1) + 2√2 = (√2-1)*√(√2-1)^2 + 2√2 =
= (√2-1)(√2-1) + 2√2 = 2-2√2+1+2√2 = 3
7) 12/(3√2) = 6/√2 = 6*√2/(√2)^2 = 6√2/2 = 3√2
8) 4/(3-√15) + 4/(3+√15) = 4(3+√15)/(9-15) + 4(3-√15)/(9-15)=
= (12+4√15+12-4√15)/(-6) = 24/(-6) = -4