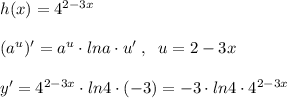
Биквадратное уравнение.
Решается заменой переменной:

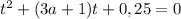
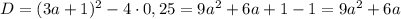
Если D >0, т.е.


уравнение имеет корни:
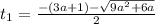 или
или 
Обратный переход:
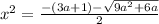 или
или 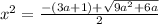
Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку
Чтобы корни данного уравнения были равны,
с=0
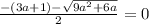
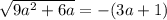
Это иррациональное уравнение.
При (3a+1) >0 оно не имеет корней.
При (3а+1) ≤0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Аналогично
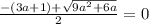
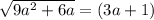
При (3a+1) < 0 оно не имеет корней.
При (3а+1) ≥0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Если  , т.е
, т.е 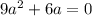
 или
или 
При 
уравнение принимает вид:

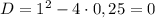 ⇒
⇒ 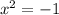
уравнение не имеет корней
При 
уравнение принимает вид:

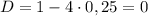 ⇒
⇒ 
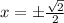
Уравнение 4-ой степени, значит
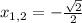 и
и 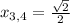
О т в е т. При 
1) а) a^2*b + a*b^2 = ab*(a+b) = 4*5 = 20
б) a^2 + b^2 = a^2 + 2ab + b^2 - 2ab = (a+b)^2 - 2ab = 5^2 - 2*4 = 17
2) а) 9^n - 2*3^n - 3 = 0
(3^n - 3)(3^n + 1) = 0
3^n + 1 > 0 при любом n.
3^n = 3
n = 1
б) 25^n - 2*5^n - 25 = 0
25^n - 2*5^n + 1 - 26 = 0
(5^n - 1)^2 - 26 = 0
(5^n - 1 - √26)(5^n - 1 + √26) = 0
5^n - 1 + √26 > 0 при любом n.
5^n = 1 + √26
n = log5 (1 + √26)
Если вы не поняли этого решения, значит, в задаче опечатка.
3) а) 6^31+6^30*5+6^29*5^2+ ... +6*5^30+5^31+5^32 =
= (6^32 - 5^32) / (6 - 5) + 5^32 = 6^32 - 5^32 + 5^32 = 6^32
б) 5^20+5^19*4+5^18*4^2+ ... +5*4^19+4^20-5^21 =
= (5^21 - 4^21) / (5 - 4) - 5^21 = 5^21 - 4^21 - 5^21 = -4^21