24 (км/час) собственная скорость яхты.
Объяснение:
Расстояние между пристанями A и B равно 143 км. Из A в B по течению реки отправился плот, а через 3 часа вслед за ним отправилась яхта, которая, прибыв в пункт B,тотчас повернула обратно и возвратилась в A. К этому времени плот км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. ответ дайте в км/ч.
Формула движения: S=v*t
S - расстояние v - скорость t – время
х - собственная скорость яхты.
х+2 - скорость яхты по течению.
х-2 - скорость яхты против течения.
143/(х+2) - время яхты по течению.
143/(х-2) - время яхты против течения.
Яхта была в пути (30:2)-3=12 (часов), уравнение:
143/(х+2)+143/(х-2)=12
Общий знаменатель (х+2)(х-2), надписываем над числителями дополнительные множители, избавляемся от дроби:
143*(х-2)+143*(х+2)=12*(х+2)(х-2)
143х-286+143х+286=12х²-48
-12х²+286х+48=0/-1
12х²-286х-48=0, квадратное уравнение, ищем корни:
D=b²-4ac = 81796+2304=84100 √D= 290
х₁=(-b-√D)/2a
х₁=(286-290)/24
х₁= -4/24 -1/6, отбрасываем, как отрицательный.
х₂=(-b+√D)/2a
х₂=(286+290)/24
х₂=576/24
х₂=24 (км/час) собственная скорость яхты.
Проверка:
143/26 + 143/22=5,5+6,5=12 (часов), верно.
х - у = 8
х + у = - 3
Выразим у из каждого уравнения:
у = х - 8
у = - х - 3
Построим графики двух этих функций. Это линейные функции, графиком являются прямые. Для построения каждой прямой надо знать две точки.
у = х – 8
х1 = 0 х2 = 1
у1 = -8 у2 = -7
(0; -8) (1; -7)
у = - х - 3
х1 = 0 х2 = 1
у1 = - 3 у2 = -4
(0; -3) (1; -4)
По данным точкам строим две прямые. Находим точку пересечения. Координаты точки пересечения будут ответом в данной системе.
х = 2,5
у = -5,5
Чертёж прилагается.
ответ: (2,5; -5,5)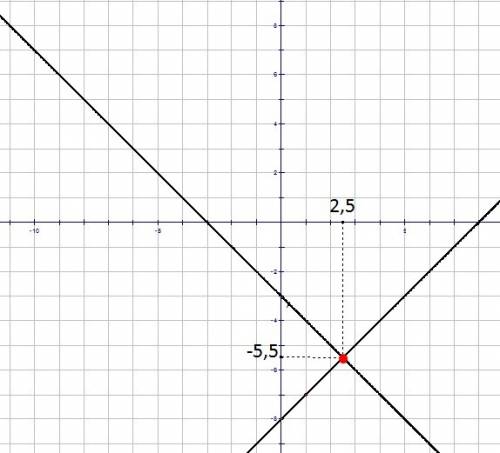
1) х-10/х-15=2
2(х-15)=х-10
2х-30=х-10
2х-х=-10+30
х=20
2) х-7/х-2=7/12
12(х-7)=7(х-2)
12х-84=7х-14
12х-7х=-14+84
5х=70
х=14