Question

Сумма координат вершины параболы y=x^2+px +q
равна 0,5, а ось ординат эта парабола пересекает в точке с ординатой 0,25. найдите абсциссу её вершины.

Answer 1

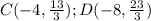
Абсцисса вершины параболы: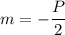 $m=-\dfrac{P}{2}$. Тогда ординату вершины параболы найдем, подставив абсциссу вершины параболы в график уравнения

$y=\left(-\dfrac{P}{2}\right)^2+P\cdot \left(-\dfrac{P}{2}\right)+Q=\dfrac{P^2}{4}-\dfrac{P^2}{2}+Q=Q-\dfrac{P^2}{4}$

По условию, сумма координат вершины параболы равна 0,5. То есть

$-\dfrac{P}{2}+Q-\dfrac{P^2}{4}=\dfrac{1}{2}~~~\bigg|\cdot 4\\ \\ -2P+4Q-P^2=2\\ \\ P^2+2P-4Q+2=0$

Далее парабола пересекает ось ординат в точке с ординатой 0,25, то есть точка (0;0.25) принадлежит параболе. Подставим их координаты

$Q=\dfrac{1}{4}$

$P^2+2P-4\cdot \dfrac{1}{4}+2=0$

$P^2+2P+1=0\\ \\ (P+1)^2=0\\ \\ P=-1$

Отсюда абсцисса вершины параболы: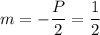 $m=-\dfrac{P}{2}=\dfrac{1}{2}$

ответ: 0,5.