a = 3
Объяснение:
Имеем выражение:
a^2 - 6 * a + 11.
Необходимо найти значение аргумента a, при котором значение выражения будет минимальным.
Здесь можно приравнивать значение выражения к нулю, можно решать квадратное уравнение, можно искать значение переменной методом подбора, но единственный практичный выделить у выражения квадрат суммы или разности двух чисел:
a^2 - 6 * a + 11 = a^2 - 2 * 3 * a + 3 * 3 + 2 = (a - 3)^2 + 2.
Получили сумму квадрата числа и двойки. Наименьшее значение суммы - 2, значит, a = 3.
;
;
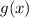и будет искомой фигурой.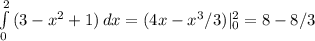
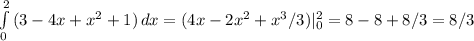
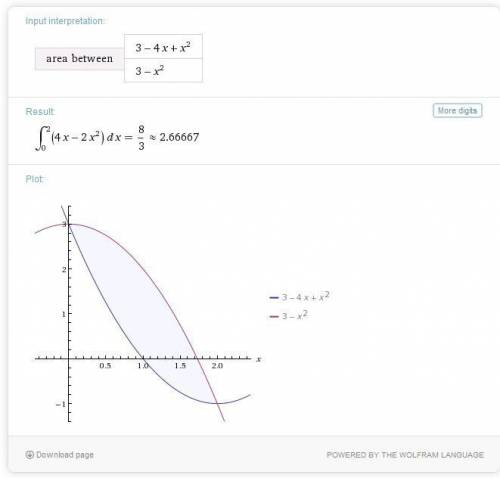
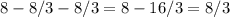(кв. ед.)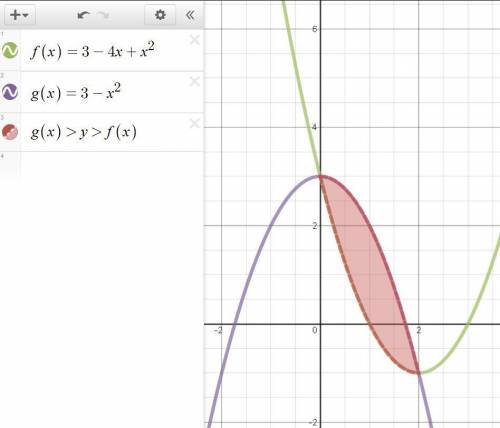
Рассуждаем так
пронумеруем игроков
1, 2, 3, 4, 5, 6, ..., n
тогда первый игрок будет играть с (n-1) человеком
второй так же и всего игроков n
Значит количество партий n(n-1) НО!
нужно Учесть что к примеру 1 игрок играет с 5 и мы посчитали эту партию в играх первого игрока, но 5 так же играет с первым и ему мы тоже эту игру посчитали. Значит одну и туже партию посчитали ДВАЖДЫ. И таких повторяющихся партий у каждого игрока
Значит общее количество партий необходимо разделить на 2
Итого количество n(n-1) /2
составим уравнение
отрицательным количество игроков быть не может
Значит ответ 16 человек приняло участие в турнире