(2; 3,5);
(1; 2);
(5;14)
Объяснение:
Пары чисел, являющихся решениями уравнения х²-2у+3=0, должны быть такими, чтобы при их подстановке в уравнение х²-2у+3 = 0, в ответе действительно получался бы 0, а не какое-то другое число.
Согласно условию задачи, необходимо выбрать пары чисел, являющихся решением уравнения х²-2у+3 = 0, из 4 следующих пар:
1) х = 2, у = 3,5;
2) х = 0, у = -1,5;
3) х = 1; у = 2;
4) х = 5; у = 14.
После подстановки этих пар чисел получаем:
1) 2²-2·3,5 +3 = 4 - 7 +3 = 7 - 7 = 0; так как полученное в результате подстановки значение действительно равно, то это говорит о том, что данная пара чисел (2; 3,5) является решением уравнения х²-2у+3=0;
2) 0²-2·(-1,5) +3 = 0 + 3 + 3 = 6; мы получили 6, но так как 6 ≠ 0, то данная пара чисел (0; -1,5) не является решением уравнения х²-2у+3=0;
3) 1²-2·2 +3 = 1 - 4 + 3 = 4 - 4 = 0; мы получили 0; т.к. 0 = 0, то данная пара чисел (1; 2) является решением уравнения х²-2у+3=0;
4) 5²-2 · 14 + 3 = 25 - 28 + 3 = 28 - 28 = 0; мы получили 0; т.к. 0 = 0, то данная пара чисел (5; 14) является решением уравнения х²-2у+3=0.
Таким образом, решениями уравнения х²-2у+3=0 являются следующие пары чисел: (2; 3,5); (1; 2); (5;14).
ответ: решениями уравнения х²-2у+3=0 являются пары чисел: (2; 3,5); (1; 2); (5;14).
а) 2x^2-11x+12=0
2x^2-3x-8x+12=0
(2x-3)*(x-4)=0
2x-3=0 или x-4=0
2x=0+3 x=4
2x=3
x=3:2
x=1,5
б) 14x^2=9x
14x^2-9x=0
x(14x-9)=0
x=0 или 14x-9=0
x=9/14
в) 16x^2-49=0
16x^2=49
x^2=49:16
x^2=49/16
x=±7/4
г) x^2-36x+323=0
x(x-17)-19(x-17)=0
(x-17)(x-19)=0
x-17=0 или x-19=0
x=17 x=19
2.
p=46=2(a+b) все это делим на 2 чтобы от нее избавиться
23=a+b
b=23-a
s=120=ab
120=a(23-a)
120=23a-a^2
-a^2+23a-120=0
d=23^2-480=529-480=49
x1=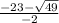
= -23-7/-2=-30/-2=15
x2=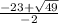
=-23+7/-2=-16/-2=8
3.x^2+px=36=0 (a=1; b=p; c=36)
d=p^2-144
12=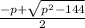
p=-15
x2=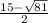
=15-9/2=6/2=3
(-1)³+5*(-1)²= -1 +5= 4