1)находим производную 3t^2+5t=6t+5
6t+5=6*2+5=17 м/с скорость в момент t=2
производная №2)6t+5=6 => уcкорение равно 6 м/с^2
2)Имеем функцию:
y = 2 * x^3 - 4 * x^2.
Напишем уравнение касательной к графику функции в точке с абсциссой x0:
y = y'(x0) * (x - x0) + y(x0);
Поэтапно находим значения функции и ее производной в точке с абсциссой x0:
y(x0) = 2 * (-1) - 4 * 1 = -2 - 4 = -6;
y'(x) = 6 * x^2 - 8 * x;
y'(x0) = 6 * 1 - 8 * (-1) = 6 + 8 = 14;
Подставляем полученные значения в формулу касательной:
y = 14 * (x + 1) - 6;
y = 14 * x + 14 - 6;
y = 14 * x + 8 - уравнение нашей касательной.
График функции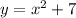
получается из графика стандартной параболы сдвигом вверх на 7 единиц по оси ординат (см. рис)
Найдем точки пересечения заданной квадратичной функции и прямой y = bx, приравняв их:
У получившегося квадратного трехчлена будет одно решение, а следовательно и и одна точка пересечения параболы и прямой при дискриминанте равном 0: