1) √19; √133
Возведем в квадрат: (√19)²; (√133)² => 19; 133
Из целых чисел, расположенных между числами 19; 133, выберем только те числа, которые являются квадратами целых чисел:
19; 20; 21; 22; 23; 24; 25; ...; 121; 122; 124; 125; 126; 127; 128; 129; 130; 131;132;133.
Это числа 25; 36; 49; 64; 81; 100; 121.
Извлечем корень из каждого из них:
5; 6; 7; 8; 9; 10; 11.
Всего 7 чисел расположено между √19 и √133.
ответ: 7.
2) 4√11 и 11√2

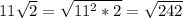
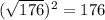
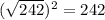
176≤x²≤242
176; 177; ...; 196;...; 225; ...;242
√196 = 14;
√225 = 15
Всего 2 числа расположено между 4√11 и 11√2.
ответ: 2.
1. Укажите линейное уравнение с двумя переменными.
1) 3·x-5=0 - только одна переменная х
2) х/7-у/5=8/3 - линейное, переменные х и у
3) 7/х+5/у=3/8 - нелинейное
4) 7·x²+5·у=3 - уравнение 2-степени
2. Укажите уравнение, решением которого является пара чисел (1 3/7; 2 5/6) .
Проверим подставкой в уравнение:
1) 14·x-12·y+14=0
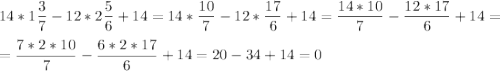
является решением, поэтому остальные уравнение не нужно проверить
2) 14·x-6·y-10=0
3) 10·x/7+17·y/6=27
4) x-6·y=17
3. Какая пара чисел является решением уравнения 3·x-2·y+5=0
1) (-1/3; -2) 2) (-2; -1/3) 3) (-4/3; -1/2) 4) (-3; 2)
Проверим подставкой в уравнение:

не является решением
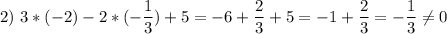
не является решением
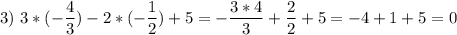
является решением, поэтому последнюю пару не нужно проверить
4. Какая из пар чисел является решением уравнением 2·x-y=6
1) (2; -1) 2) (5; 3) 3) (1; -4) 4) (-1; -3)
Проверим подставкой в уравнение:
1) 2·2-(-1)=4+1=5≠6 - не является решением
2) 2·5-3=10-3=7≠6 - не является решением
3) 2·1-(-4)=2+4=6=6 - является решением, поэтому последнюю пару не нужно проверить
ответ: 7 целых чисел: 5,6,7,8,9,10,11.
2)
ответ: 2 целых числа: 14 и 15