я подозреваю что тут закралась неясность, в прогрессии насколько я помню количество элементов бесконечно, хотя в убывающей геометрической прогресии сумма всех элементов может сходиться.
инфми словами условие следует понимать так что n первых членов прогресии, где n = 2k,
выполняется условие 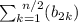 в три раза больше, чем
в три раза больше, чем 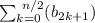
рассмотрим это более подробно на примере первых шести элементов
сумма нечетных S(1,3,5) = b1 + b3 + b5
сумма четных S(2,4,6) = b2 + b4 + b6 = b1*q + b3*q + b5*q = q(b1 + b3 + b5) = q*S(1,3,5)
следовательно отношение между четной суммой и нечетной равно знаменателю прогрессии.
Для нашей задачи это число 3
ответ 3
Відповідь:
Пояснення:
1)Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 32 - 4·1·(-54) = 9 + 216 = 225
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = ( -3 - √225) /2·1 = ( -3 - 15)/ 2 = -18 /2 = -9
x2 = ( -3 + √225) /2·1 = ( -3 + 15) /2 = 12/ 2 = 6
2)-7x2 - 3x = 0
Найдем дискриминант
D = b2 - 4ac = (-3)2 - 4·(-7)·0 = 9 - 0 = 9
x1 = (3 - √9)/ 2·(-7) = (3 - 3) /-14 = 0/ -14 = 0
x2 = (3 + √9)/ 2·(-7) = ( 3 + 3)/ -14 = 6 /-14 = - 3 /7
3)x^2=16
x=4
4)D = b2 - 4ac = 12 - 4·1·(-56) = 1 + 224 = 225
x1 = (-1 - √225)/ 2·1 = ( -1 - 15 )/2 = -16 /2 = -8
x2 = ( -1 + √225)/2·1 = ( -1 + 15) /2 = 14/ 2 = 7
5)D = b2 - 4ac = (-4)2 - 4·1·(-5) = 16 + 20 = 36
x1 = ( 4 - √36)/ 2·1 = ( 4 - 6)/ 2 = -2 /2 = -1
x2 = ( 4 + √36)/ 2·1 = ( 4 + 6)/ 2 = 10/ 2 = 5
Характеристическое уравнение однородного диф. уравнения имеет вид:
Найдем частное решение неоднородного уравнения в виде
u=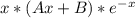
производная u=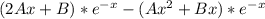
вторая производная u=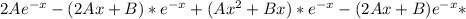
Подставляя в исходное уравнение производные имеем систему уравнений: УРАВНЕНИЕ ПРИ СТЕПЕНИ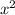 имеет вид 5А-6А+А=0, 0А=0, верно при любом значении А.
имеет вид 5А-6А+А=0, 0А=0, верно при любом значении А.
Имеем: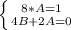
Таким образом, общее решение исходного уравнения имеет вид: