Одно: n = 9376
Объяснение:
n(n-1) делится на 10^4.
Если одно из чисел (n или n-1) не делится ни на 2, ни на 5, то оно взаимно просто с 10000, и другое число обязано делиться на 10000. Очевидно, таких четырехзначных n, что n или n-1 делится на 10000, нет. Значит, оба числа делятся на 2 или на 5. Два числа вместе делиться на 2 или на 5 не могут, т.к. различаются на 1. Значит, одно из них делится на 2 (не делится на 5), а другое на 5 (не делится на 2).
Пусть, n =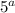 
* b (a - степень вхождения 5 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 5, поэтому, чтобы n(n-1) делилось на 
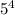, нужно чтобы а было ≥ 4.
n ≡ 0 mod .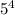
Аналогично n-1 ≡ 0 mod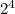 
(т.к. n не делится на 2) ⇒ n ≡ 1 mod 2^4
Видно, что n = 625 подходит. По кит. т. об остатках, все остальные n получаются прибавлением константы 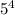* 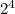= 10000, умноженной на целое число. Значит, таких четырехзначных n не существует.
Пусть, n =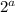 
* b (a - степень вхождения 2 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 2, поэтому, чтобы n(n-1) делилось на 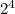, нужно чтобы а было ≥ 4.
n ≡ 0 mod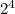
Аналогично n-1 ≡ 0 mod 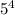(т.к. n не делится на 5) ⇒ n ≡ 1 mod 5^4
Видно, что n = 9376 подходит. По кит. т. об остатках, все остальные n получаются прибавлением константы 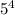* 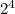= 10000, умноженной на целое число. Значит, существует только 1 четырехзначное n = 9376.
Если моё решение Вам отметьте его как лучшее.
Здесь надо понять две вещи. и тогда Вы не будете просить о
1 угловой коэффициент отвечает за тупость, остроту или прямоту.) шучу.
если угловой коэффициент положителен, то угол наклона прямой к положительному направлению оси ох острый. если меньше нуля. то тупой. если равен нулю, то прямая параллельна оси ох.
2. ордината точки пересечения может находиться выше оси ох, на ней или ниже. если выше, то b в уравнении y=ax+b положительно, если ниже, то отрицательно. если равно нулю. то на оси ох.
Теперь по вашим картинкам.
1. А, Б- отрицательные коэффициенты, их легко найти по Вашим подсказкам и проверить. А соответствует угловой коэффициент тангенс угла наклона прямой. он равен пяти, Б угловой коэффициент равен -4/5, или -0.8, для оставшихся двух прямых В соответствует угловому коэф. 1, и Г угловому коэффициенту 4/3
Собираем замеченное выше, формируем ответ.)
1 -Г
2-А
3-Б
4-В