1)
2а(а+b)-b(2a-b)-b(b+1) = 2a² + 2ab - 2ab + 2b² - b² - b = 2a² + b² - b = (-0,3)² + (-0,4)² - (-0,4) = 0,09 + 0,16 + 0,4 = 0,65
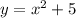- квадратичная функция, график парабола, ветви вверх. Находишь вершину параболы, она соответственно имеет координаты (0; 5). Далее просто каждому значению X находишь значение Y - это и будут точки, по которым строить параболы. Вообще, тебе нужно нарисовать обычную параболу с уравнением 
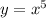, только на 5 условных единиц (например клеток, если ты 1 клетку взял на единицу) выше.
Для твоей параболы следующие точки с целочисленными значениями: (1; 6), (-1; 6), (2; 9); (-2; 9) и сама вершина (0;5), далее рисуешь "ветви" направленные вверх и график готов.
√(4x² - 121) + |x² + 2x - 63| = 0
товарищ верь ! взойдет она, звезда пленительного счастья напишут наши имена.
Слева 2 неотрицательных слагаемых . значит сумма равна 0, только тогда когда
√(4x² - 121) = 0 и |x² + 2x - 63| = 0
ищем корни
x² + 2x - 63 = 0
D = 4 + 4*63 = 256 = 16²
x12 = (-2 +- 16)/2 = -9 7
Сравним с другими корнями
4x² - 121 = 0
x² = 121/4
x12 = +- 11/2
корни не совпадают
значит сумма всегда не равна 0
корней нет
решений нет
вот если
Вместо √(4x² - 121) было бы √(4x² - 144) то корень x = +- 7 сумма 7, а было бы √(4x² - 324) то корень х = +- 9 сумма -9
при а=-0,3; b=-0,4
2a^2+b=2*(-0,3)^2*(-0,4)-0,4= 0,072-0,4=0,328