Объяснение:
1) число вариантов выбора 5 солдат из 8 это число сочетаний из 8 по 5
С⁵₈=8!/(5!*(8-5)!)=8!/(5!*3!)=1*2*3*4*5*6*7*8/(1*2*3*4*5*1*2*3)=
=6*7*8/(2*3)=56 вариантов
2) число вариантов выбора 2 офицеров 4 это число сочетаний из 4 по 2
С²₄=4!/(2!*(4-2)!)=4!/(2!*2!)=1*2*3*4/(1*2*1*2)=2*3=6 вариантов
на каждый из 56 вариантов выбора солдат приходится 6 вариантов выбора офицеров, тогда число составить дозор из 5 солдат и 2 офицеров при наличии 4 офицеров и 8 солдат будет равно произведению
56*6=336
Объяснение:
Надо найти сколькими из 4-х человек можно отобрать 2, то есть найти число сочетаний из 4 по 2 - это будет . Решение на картинке.
Если объяснять словами то есть 4 человека 1,2,3,4. В первый отряд мы можем взять (1 и 2), (1 и 3), (1 и 4), (2 и 3), (2 и 4), и (3 и 4) - это и будет .
Теперь найдем сколькими можно сочетать оставшиеся 12 человек по 6, то есть сколькими можно их разделить на 2 равных отряда. Это . Решение на второй картинке.
И, что бы окончательно решить, сколькими можно распределить 12 человек не знающих местность и 4 человек знающих местность нужно перемножить полученные результаты:
6*66 = 396 - это и будет общее количество , которыми можно разделить 16 человек на 2 отряда по 8 человек, что бы в каждом отряде было 2 человека знающих местность и 6 человек не знающих местность.

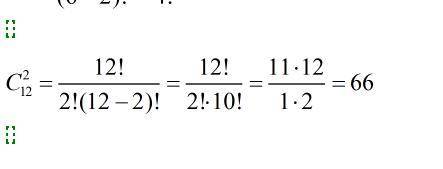
1). Правильными называются дроби, у которых числитель меньше знаменателя. Таких в условии всего две: 18/42; 16/28.
2). 1/10 · 3 = 3/10
3). 5/14 · 9/10 = 1/14 · 9/2 = 9/28
4). 2/7 · 9/10 · 1/14 = 18/980 = 9/490
5). 5/12 : 9 = 5/12 · 1/9 = 5/108
6). 33/56 : 9/14 = 33/56 · 14/9 = 11/4 · 1/3 = 11/12
7). 8/11 : 25/11 : 3/5 = 8/11 · 11/25 · 5/3 = 8/25 · 5/3 = 8/15
8). 5/4 = 1 1/4
9). 5 11/4 = 31/4
10). 2 1/24 · 1 5/7 = 49/24 · 12/7 = 7/2 = 3 1/2
11). 10 5/12 : 2 1/2 = 125/12 · 2/5 = 25/6 = 4 1/6
12). 1 4/5 · p + 1 5/6 = 9/5 · 5 + 1 5/6 = 9 + 1 5/6 = 10 5/6