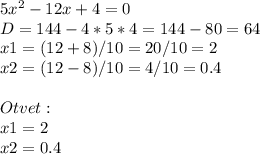
5x²-12x+4=0
D=144-80=8²
x1=(12+8)/10=2
x2=(12-8)/10=0.4
ответ: 0.4,2
обозначим отрезки дороги a-ровная, b-в гору (обратно с горы), с-с горы (обратно в гору)
Расстояние между городами х
Не учитывая направления движения найдем среднуюю скорость при движении на участке b
Этот участок автобус проходит два раза.
Vср=2b/(b/30+b/60)=2b/(3b/60)=40 км/ч
Все тоже самое справедливо для участка с.
Значит и там средняя скорость равна 40 км/ч.
Ровные и неровные участки равны.
Составляем уравнение, учитывая, что х-расстояние между городами проезжам два раза и делим на два участка. То есть изначально уравнение выглядит так:
2x/(2*50)+2x/(2*40)=2.25
x/50+x/40=2.25
0.02x+0.025x=2.25
0.045x=2.25
x=50
Получается 50 км.
f(x) = корень(9-12x+4x^2)/корень(9+12x+4x^2)-24x/(9-4x^2)+2x/(3-x)
Перед тем как найти производную упростим выражение
корень(9-12x+4x^2)/корень(9+12x+4x^2) = корень((2x-3)^2)/корень((2x+3)^2) =
(2x-3)/(2x+3) ( в числителе (2х-3) так как х=2,5 а корень>0
корень(9-12x+4x^2)/корень(9+12x+4x^2)-24x/(9-4x^2)+2x/(3-x ) =
= (2x-3)/(2x+3)+24x/(4x^2-9) +2x/(3-x) = (2x-3)/(2x+3)+24x/((2x-3)(2x+3)) +2x/(3-x) =
= ((2x-3)^2+24x)/((2x-3)(2x+3)) +2x/(3-x) = (4x^2+12x+9)/((2x-3)(2x+3)) +2x/(3-x) =
=(2x+3)^2/((2x-3)(2x+3)) +2x/(3-x) = (2x+3)/(2x-3) +2x/(3-x)
Теперь найдем производную
y' = (2(2x-3)-(2x+3)*2)/(2x-3)^2 +(2(3-x)-2x(-1))/(3-x)^2 =
=-12/(2x-3)^2 +6/(3-x)^2
при х =2,5
y'(2,5) = -12/(2*2,5-3)^2 +6/(3-2,5)^2 = -12/4+6/(1/4) =-3+24 =21