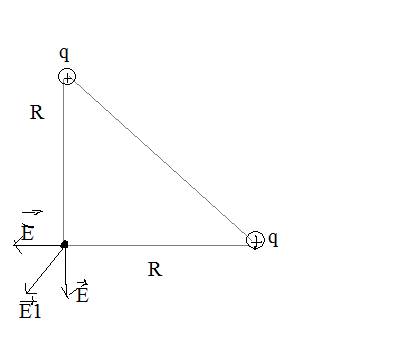
1)в векторном виде (рисунок во вложениях) : E=E1+E2 - т.к. заряды в вершинах равны и расстояние до третьей вершины, то Е1=Е2
в модульном виде E^2=E1^2+E1^2
E=E1*корень2
корень2=1.4
Е2=E1=kq/R^2 - напряженность
тогда E=1.4kq/R^2=1.5*9*10^9*3*10^-7/0.1^2=4.1*10^4 В/м
2)ф=ф1+ф2 - принцип суперпозиции
ф1=ф2=kq/r
ф=2ф1=2kq/r=2*9*10^9*3*10^-7/0.1=5.4*10^4 B
3) F=F1+F2 - в векторном виде (рисунок как во вложениях, только вместо Е - F)
F^2=F1^2+F2^2 - модульный вид
F1=F2 - равны
F=F1корень2
корень2=1.4
F1=kqq1/R^2
F=1.4*kqq1/R^2=1.4*9*10^9*3*10^-7*10^-8/0.1^2=3.8*10^-3 H
Объяснение:
1. Изотермическое расширение (на рис. 1 — процесс A→Б/A→B). В начале процесса рабочее тело имеет температуру {\displaystyle T_{H}}T_{H}, то есть температуру нагревателя. При расширении рабочего тела его температура не падает за счет передачи от нагревателя количества теплоты {\displaystyle Q_{H}}Q_{H}, то есть расширение происходит изотермически (при постоянной температуре) . При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.
2. Адиабатическое расширение (на рис. 1 — процесс Б→В/B→C). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника {\displaystyle T_{X}}T_{X}, тело совершает механическую работу, а энтропия остаётся постоянной.
3. Изотермическое сжатие (на рис. 1 — процесс В→Г/C→D). Рабочее тело, имеющее температуру {\displaystyle T_{X}}T_{X}, приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты {\displaystyle Q_{X}}Q_{X}. Над телом совершается работа, его энтропия уменьшается.