Раз мы ищем минимальный период, значит расстоянием от поверхности звезды до спутника можно пренебречь по сравнению с радиусом R самой звезды.
Сила притяжения равна центростремительной силе:
GMm/R² = mω²R, здесь М - масса звезды, а м - масса спутника. G - гравит. постоянная.
С учетом того, что круговая частота выражается через период:
ω = 2π/T,
а масса звезды выражается через плотность и объем:
M = ρ*V = (4πR³ρ)/3,
получим:
Gρ/3 = π/T²
Отсюда находим искомый минимальный период:
T = √[3π/(Gρ)] = √[3*3,14/(6,67*10^(-11) *10^17) ≈ 1,2*10^(-3) c = 1,2 мс
Окей, друзья. Начнем. Какая у нас формула максимальной дальности полета тела, брошенного под углом к горизонту:
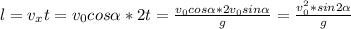
Максимальной она будет, если значение синуса максимально. А макс. значение синуса = 1. Т.е.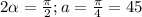
градусов
Теперь вычислим из этой формулы нулевую скорость:
Теперь займемся нашим выстрелом, когда марсоход в движении. Опять же максимальная дальность будет, если угол выстрела = 45 градусов. Однако скорости не сложатся, надо высчитать итоговую нулевую скорость снаряда: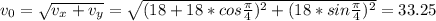
м/c.
Теперь рассчитаем максимальную дальность:
ответ 276 метров.