Если коротко, то свет распространяется быстрее, чем звук.
На самом деле в том месте, где появляется молния гром можно услышать одновременно сней, так как это части одного процесса. Как-то очень давно молния ударила сравнительно недалеко от меня - так вот я не заметил никакой разницы во времени между молнией и громом.
Мы видим молнию, потому что до нас долетает свет от разряда. Мы слышим гром, потому что до нас доходит его звуковая ударная волна. Свет распространяется намного быстрее звука, поэтому мы сначала видим молнию, а только потом слышим гром.
Для примера, если мы будем стоять на некотором расстоянии друг от друга и Вы будете моргать мне фонариком. то эти сигналы я увижу практически сразу. Но вот если вместо этого Вы решите добежать до меня, то на это уже понадобится некотрое время. Так и звуку грома требуется время на то, чтобы долететь до Вашего уха, тогда как вспышка молнии видна глазу практически мгновенно.
Дано:
F = 4 см
f = 12 см
Δs = 3 см
ΔS - ?
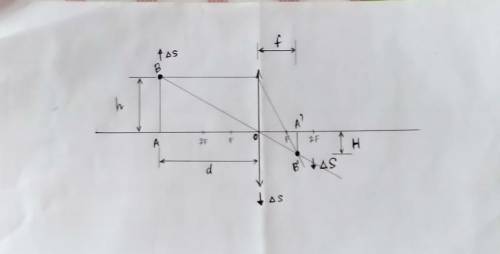
При данных условиях - точка на расстоянии 12 см, т.е. больше двойного фокусного расстояния (12 см > 2*4 см), и выше оптической оси - изображение точки находится на расстоянии гораздо меньшем от оси, причём располагается под осью, т.к. является перевёрнутым. Мы можем опустить перпендикуляры от точки до оси и от изображения точки до оси. Эти перпедикуляры будем считать высотами точки и её изображения:
h - высота точки
Н - высота изображения
По формуле линейного увеличения линзы выясним отношение Н к h:
Г = Н/h
Из свойств подобных треугольников следует, что отношение стороны одного из них к такой же стороне другого треугольника равно отношению двух других сторон треугольников. H и h - это противолежащие катеты двух прямоугольных треугольников А'В'О и АВО, а f и d - их прилежащие катеты, f - расстояние от изображения точки до линзы, d - расстояние от точки до линзы. Поэтому:
Г = H/h = f/d
Найдём f по формуле тонкой линзы:
1/f + 1/d = 1/F
1/f = 1/F - 1/d = (d - F)/Fd
f = Fd/(d - F)
Подставим это выражение в формулу увеличения линзы:
Г = Н/h = f/d = (Fd/(d - F)) : d = Fd/((d - F)d) = F/(d - F)
Выразим высоту изображения точки:
Г = Н/h => H = hГ = Fh/(d - F)
Если двигать линзу вверх-вниз, то отношение высот Н и h не поменяется, т.е. формула линейного увеличения линзы будет работать и после её перемещения вниз на Δs. Точка остаётся на месте, но относительно линзы, а значит относительно и оптической оси, она перемещается на такое же расстояние Δs, только вверх. А расстояние от точки до оси - это перпендикуляр, который мы условились считать высотой h. Следовательно новая высота h' после перемещения линзы равна:
h' = h + Δs
Подставим это в формулу для Г':
Г' = Г = H'/h' = H'/(h + Δs) = F/(d - F)
Выражаем H':
H' = (h + Δs)*F/(d - F) = (Fh + FΔs)/(d - F)
Расстояние ΔS, на которое переместится изображение точки на экране, равно изменению высоты изображения:
ΔS = ΔH = H' - Н = ((Fh + FΔs)/(d - F)) - (Fh/(d - F)) = (Fh + FΔs - Fh)/(d - F) = FΔs/(d - F) = 4*3/(12 - 4) = 12/8 = 3/2 = 1,5 см
ответ: на 1,5 см.